You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is the frequency of a police siren when you run away from it?
- Thread starter ThePhysicsXV
- Start date
-
- Tags
- Frequency
AI Thread Summary
The discussion revolves around calculating the frequency of a police siren as it approaches an observer running away from it, using the Doppler effect formula. The police car emits a siren at 988 Hz while traveling at 23 m/s, and the observer runs away at 7 m/s. Participants clarify the roles of the source (the siren) and the observer, emphasizing the need to consider their motions separately. The speed of sound at 28°C is calculated to be 348 m/s, and the correct application of the Doppler effect formula yields a frequency of approximately 1036.64 Hz as the police car approaches the observer. The conversation concludes with participants confirming the accuracy of the calculations and expressing gratitude for assistance.
Physics news on Phys.org
vela
Staff Emeritus
Science Advisor
Homework Helper
- 16,203
- 2,854
What specifically is confusing you?
ThePhysicsXV
- 35
- 0
I know how to solve to get the speed of sound but are they moving forward (+) or backward (-) and what's is the observer and source. Is the source the police siren?vela said:What specifically is confusing you?
ThePhysicsXV
- 35
- 0
Do I use the formula I gave or the one from the picture?vela said:What specifically is confusing you?
vela
Staff Emeritus
Science Advisor
Homework Helper
- 16,203
- 2,854
The observer is what detects the sound. The source is what produces the sound the observer hears.
Consider the two motions separately. What effect does the motion of the police car have on the frequency detected, and what effect does your movement have on the frequency detected?
Consider the two motions separately. What effect does the motion of the police car have on the frequency detected, and what effect does your movement have on the frequency detected?
ThePhysicsXV
- 35
- 0
vela said:The observer is what detects the sound. The source is what produces the sound the observer hears.
Consider the two motions separately. What effect does the motion of the police car have on the frequency detected, and what effect does your movement have on the frequency detected?
So is V = 988(348+7/ 348+8)
Or V=988(348-7/348-23)?
ThePhysicsXV
- 35
- 0
348m/s is the speed of soundThePhysicsXV said:So is V = 988(348+7/ 348+8)
Or V=988(348-7/348-23)?
vela
Staff Emeritus
Science Advisor
Homework Helper
- 16,203
- 2,854
Instead of plugging numbers in randomly, please answer the questions.
ThePhysicsXV
- 35
- 0
I have no idea how to answer your question.vela said:Instead of plugging numbers in randomly, please answer the questions.
- 42,643
- 10,431
How would you "solve to get the speed of sound"? The speed of sound is a given.ThePhysicsXV said:I know how to solve to get the speed of sound but are they moving forward (+) or backward (-) and what's is the observer and source. Is the source the police siren?
As vela says, the source is the siren, you are the observer.
Are the source and observer moving in the same direction or in opposite directions?
As vela suggests, try it in two parts. First, what frequency did you hear before starting to run? Can you quote an equation for the Doppler effect?
ThePhysicsXV
- 35
- 0
The source and observer are moving on the same direction since the police car coming toward you, and you getting away.haruspex said:How would you "solve to get the speed of sound"? The speed of sound is a given.
As vela says, the source is the siren, you are the observer.
Are the source and observer moving in the same direction or in opposite directions?
As vela suggests, try it in two parts. First, what frequency did you hear before starting to run? Can you quote an equation for the Doppler effect?
V sound in air = 331.4 + 0.6T
T is temperature so temp=28
And you will get 348m/s
- 42,643
- 10,431
Ok, but what about the Doppler effect? So far, I see no evidence that you've even heard of it.ThePhysicsXV said:The source and observer are moving on the same direction since the police car coming toward you, and you getting away.
V sound in air = 331.4 + 0.6T
T is temperature so temp=28
And you will get 348m/s
ThePhysicsXV
- 35
- 0
haruspex said:Ok, but what about the Doppler effect? So far, I see no evidence that you've even heard of it.
Doppler Effect for Moving Source and Observer
ƒ'=ƒ((1±u₀/v)/(1±u(sound)/v))
- 42,643
- 10,431
Ok, so apply that.ThePhysicsXV said:Doppler Effect for Moving Source and Observer
ƒ'=ƒ((1±u₀/v)/(1±u(sound)/v))
ThePhysicsXV
- 35
- 0
Actually they both moving at different speeds. Police at 23m/s and "you" at 7m/sharuspex said:Ok, so apply that to the case where the car is approaching you but you are standing still.
- 42,643
- 10,431
Yes, I replied a little too quickly, then edited it.ThePhysicsXV said:Actually they both moving at different speeds. Police at 23m/s and "you" at 7m/s
I anticipated that you would quote a formula for only one movement, so I was trying to get you to solve it in the two stages, as vela had suggested. When I realized your equation allowed for both moving I edited my post, but you were too quick for me.
So, apply the equation.
ThePhysicsXV
- 35
- 0
haruspex said:Yes, I replied a little too quickly, then edited it.
I anticipated that you would quote a formula for only one movement, so I was trying to get you to solve it in the two stages, as vela had suggested. When I realized your equation allowed for both moving I edited my post, but you were too quick for me.
So, apply the equation.
f=988(348+7/348+23)
f= 945Hz
ThePhysicsXV
- 35
- 0
haruspex said:Yes, I replied a little too quickly, then edited it.
I anticipated that you would quote a formula for only one movement, so I was trying to get you to solve it in the two stages, as vela had suggested. When I realized your equation allowed for both moving I edited my post, but you were too quick for me.
So, apply the equation.
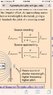
Attachments
- 42,643
- 10,431
I did have some concerns about the equation you posted previously, but I wanted to see how you applied it. The equations in the image you have attached look fine, except that you should ignore the references to "Stationary" observer. That makes no sense given the rest of the text. It's probably a cut-and-paste error from some preceding cases.
So, which of the two cases in the image do you think applies here? What do you get when you apply it?
So, which of the two cases in the image do you think applies here? What do you get when you apply it?
ThePhysicsXV
- 35
- 0
f= f(v-o/v-s)haruspex said:I did have some concerns about the equation you posted previously, but I wanted to see how you applied it. The equations in the image you have attached look fine, except that you should ignore the references to "Stationary" observer. That makes no sense given the rest of the text. It's probably a cut-and-paste error from some preceding cases.
So, which of the two cases in the image do you think applies here? What do you get when you apply it?
I got 1036.64Hz
- 42,643
- 10,431
I get the same. Round that to the appropriate number of digits.ThePhysicsXV said:f= f(v-o/v-s)
I got 1036.64Hz
ThePhysicsXV
- 35
- 0
Okay, I guess that's the correct answer. But Thank you sir for your helpharuspex said:I get the same. Round that to the appropriate number of digits.
Similar threads
- Replies
- 6
- Views
- 6K
- Replies
- 5
- Views
- 2K
- Replies
- 3
- Views
- 8K
- Replies
- 2
- Views
- 1K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 6
- Views
- 11K
- Replies
- 1
- Views
- 3K
- Replies
- 2
- Views
- 2K
- Replies
- 1
- Views
- 2K
Hot Threads
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math