What is the Length of a Parabolic Segment Using Calculus 3?

[GreenPrint]

Homework Statement

Find the length of the parabolic segment r = $\frac{12}{1+cos(θ))}$, 0$\leq$θ$\leq$$\frac{∏}{2}$.

Homework Equations

L = ∫$\sqrt{f(θ)^{2}+f^{'}(θ)^{2}}$dθ

The Attempt at a Solution

I got up to here and didn't know whta to do

L = 12 $∫^{0}_{\frac{∏}{2}}$ $\frac{1}{1+cos(θ)}$$\sqrt{1+(\frac{sin(θ)}{1+cos(θ)})^{2}}$dθ

Wolfram alpha doesn't know neither

$f(θ)^{2}$ = $(\frac{12}{1+cos(θ))})^{2}$
$f^{'}(θ)^{2}$ = $(\frac{12sin(θ)}{(1+cos(θ))^{2}})^{2}$
$\sqrt{f(θ)^{2}+f^{'}(θ)^{2}}$ = $\sqrt{(\frac{12}{1+cos(θ))})^{2}+(\frac{12sin(θ)}{(1+cos(θ))^{2}})^{2}}$=$\frac{12}{1+cos(θ)}\sqrt{1+(\frac{sin(θ)}{1+cos(θ)})^{2}}$

 

[Ray Vickson]

Homework Statement

Find the length of the parabolic segment r = $\frac{12}{1+cos(θ))}$, 0$\leq$θ$\leq$$\frac{∏}{2}$.

Homework Equations

L = ∫$\sqrt{f(θ)^{2}+f^{'}(θ)^{2}}$dθ

The Attempt at a Solution

I got up to here and didn't know whta to do

L = 12 $∫^{0}_{\frac{∏}{2}}$ $\frac{1}{1+cos(θ)}$$\sqrt{1+(\frac{sin(θ)}{1+cos(θ)})^{2}}$dθ

Wolfram alpha doesn't know neither

Mod note: Fixed incorrect = in the identity below.[/color]
First, simplify the integrand using trig identities such as $\sin^2(\theta) + \cos^2(\theta) = 1.$ After that, Maple manages to do the integral, but I won't report the answer here: you can try again after simplification, substitution, etc. BTW: to get $\int_{0}^{\pi/2}$ you need to type \int_{0}^{\pi/2}, not what you typed.

RGV

 

[GreenPrint]

oh hm ok thanks i got to go ill be back later

 

[GreenPrint]

well i tired to simplify it further but keep on getting stuck

12 square root (2) * integral[0,pi/2] d theta/(sin(theta)+sin(2*theta))

is as far as i got

 

[GreenPrint]

I entered a approximation into the answer box and it told me i was wrong so i guess it wants a exact answer

here is what it said (see attachment) I'm not sure it really helps

also note that I tried to evaluate
12 square root (2) * integral[0,pi/2] d theta/(sin(theta)+sin(2*theta))
using trig substitution with angle alpha
cot(alpha)^2/2 = cos(theta)
I would have to solve for theta
and then find d theta/ d alpha
solve for d alpha
and use the fact that
cos(alpha)^2/sin(theta) = 1/(sin(theta)+sin(2theta))
but I'm not sure if this will all work

i believe that it's equivalent
that is 12 square root (2) * integral[0,pi/2] d theta/(sin(theta)+sin(2*theta))

 

[GreenPrint]

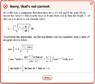
So here is were I'm at now

L = 12 $∫^{\frac{∏}{2}}_{0}$ $\frac{1}{1+cos(θ)}$$\sqrt{1+(\frac{sin(θ)}{1+cos(θ)})^{2}}$dθ

from here I used the fact that
1 + cos(θ) = 2$cos^{2}$($\frac{θ}{2}$)
so
$\frac{sec^{2}(\frac{θ}{2})}{2}$ = $\frac{1}{1+cos(θ)}$
similarly
$\sqrt{1+(\frac{sin(θ)}{1+cos(θ)})^{2}}$ = $\sqrt{1+\frac{sec^{4}(\frac{θ}{2})sin^{2}(θ)}{4}}$
So I know have the following

L = 12 $∫^{\frac{∏}{2}}_{0}$ $\frac{1}{1+cos(θ)}$$\sqrt{1+(\frac{sin(θ)}{1+cos(θ)})^{2}}$dθ = 12 $∫^{\frac{∏}{2}}_{0}$ $\frac{sec^{2}(\frac{θ}{2})}{2}$ $\sqrt{1+\frac{sec^{4}(\frac{θ}{2})sin^{2}(θ)}{4}}$dθ
from here I use the fact that
$sin^{2}$(θ)=4$sin^{2}$($\frac{θ}{2}$)$cos^{2}$($\frac{θ}{2}$)
wolfram alpha confirm it's true
http://www.wolframalpha.com/input/?i=sin(x)^2=4sin(x/2)^2*cos(x/2)^2
plugging this in I get

12 $∫^{\frac{∏}{2}}_{0}$ $\frac{sec^{2}(\frac{θ}{2})}{2}$ $\sqrt{1+sec^{4}(\frac{θ}{2})sin^{2}(\frac{θ}{2})cos^{2}(\frac{θ}{2})}$dθ=6 $∫^{\frac{∏}{2}}_{0}$ $sec^{2}(\frac{θ}{2})$$\sqrt{1+sec^{2}(\frac{θ}{2})sin^{2}(\frac{θ}{2})}$dθ, u = $\frac{θ}{2}$, $\frac{du}{dθ}$=$\frac{1}{2}$,du=$\frac{dθ}{2}$,dθ=2du,L=12 $∫^{θ=\frac{∏}{2}}_{θ=0}$ $sec^{2}(u)$$\sqrt{1+sec^{2}(u)sin^{2}(u)}$du=12 $∫^{θ=\frac{∏}{2}}_{θ=0}$ $sec^{2}(u)$$\sqrt{1+tan^{2}(u)}$du
then from here I use
$sin^{2}(θ)$)+$cos^{2}(θ)$=1
that if I divide through by $cos^{2}(θ)$ I get
$tan^{2}(θ)$)+1=$sec^{2}(θ)$
L=12 $∫^{θ=\frac{∏}{2}}_{θ=0}$ $sec^{2}(u)$$\sqrt{sec^{2}(u)}$du=12$∫^{θ=\frac{∏}{2}}_{θ=0}$ $sec^{3}(u)$du
then because
∫$sec^{n}(x)dx = \frac{sec^{n-2}(x)tan(x)}{n-1}+\frac{n-2}{n-1}∫sec^{n-2}(x)dx$
we got
12$∫^{θ=\frac{∏}{2}}_{θ=0}$ $sec^{3}(u)du=12[\frac{sec(u)tan(u)}{2}+\frac{1}{2}∫sec(u)du]|^{θ=\frac{∏}{2}}_{θ=0}$
and because
∫sec(x)dx=ln|sec(x)+tan(x)|+c
we got
$12[\frac{sec(u)tan(u)}{2}+\frac{1}{2}∫sec(u)du]|^{θ=\frac{∏}{2}}_{θ=0}=12[\frac{sec(u)tan(u)}{2}+\frac{1}{2}ln(|sec(u)+tan(u)|)]|^{θ=\frac{∏}{2}}_{θ=0}$
plugging back in
u = $\frac{θ}{2}$
we got
$12[\frac{sec(u)tan(u)}{2}+\frac{1}{2}ln(|sec(u)+tan(u)|)]|^{θ=\frac{∏}{2}}_{θ=0}=12[\frac{sec(\frac{θ}{2})tan(\frac{θ}{2})+ln|sec(θ/2)+tan(\frac{θ}{2})|}{2}]|^{θ=\frac{∏}{2}}_{θ=0}=12[\frac{sec(\frac{∏}{4})tan(\frac{∏}{4})+ln(|sec(∏/4)+tan(\frac{∏}{4})|)}{2}-\frac{sec(0)tan(0)+ln(|sec(0)+tan(0)|}{2})=12[\frac{\sqrt{2}+ln(|\sqrt{2}+1|)}{2}-0]$=6($\sqrt{2}$+ln($\sqrt{2}+1)$)

 

[Mark44]

I haven't worked the problem through, but here is what I got.

r² + (r')² = $$\frac{288}{(1 + cosθ)^3}$$

You still need to take the square root, and then integrate that result. No doubt another trig identity will come in useful.

 

[GreenPrint]

I have no idea how you got that. I get

$\frac{144}{(1+cos(θ))^{2}}$ + $\frac{144(1-cos^{2}(θ))}{(1+cos(θ))^{4}}$ = $\frac{144}{(1+cos(θ))^{2}}(1+$$\frac{1-cos^{2}(θ)}{(1+cos(θ))^{2}}$)

when I try to expand it

 

[GreenPrint]

well i found one mistake in my work i forgot to square the two let's see...

 

[Mark44]

I have no idea how you got that. I get

$\frac{144}{(1+cos(θ))^{2}}$ + $\frac{144(1-cos^{2}(θ))}{(1+cos(θ))^{4}}$ = $\frac{144}{(1+cos(θ))^{2}}(1+$$\frac{1-cos^{2}(θ)}{(1+cos(θ))^{2}}$)

when I try to expand it

In the first line above, 1 - cos²θ = sin²θ, right?

 

[GreenPrint]

yes...
if you see I believe I had the right answer above... I actually got an answer which is a improvement...
I got the integral of sec^3(x) dx
but I get the wrong answer did I use the wrong reduction formula or something =( I think it's the right reduction formula but I'm not sure

 

[GreenPrint]

ok well i did use the right reduction formula
at first i had tan(pi/4)=sqrt(2)/2 but it's one i fixed that and updated my answer above
I don't see what I've done wrong but apparently it is
my calculator gives me 13.77735
and when i put in the answer i got i get 7.4787

 

[Mark44]

I checked what I had in wolframalpha, and got 13.7735 (two 7's, not 3), which sort of agrees with your calculator answer.

You have a ton of stuff in post #6, too much to wade through to find an error.

The integral should look like this, if my work is correct:
$$12\sqrt{2}\int_0^{\pi/2} \frac{d\theta}{(1 + cos\theta)^{3/2}}$$

There's a half-angle identity that might be useful here: cosθ + 1 = 2 cos²(θ/2). This turns the integral above into
$$12\sqrt{2}\int_0^{\pi/2} \frac{d\theta}{(2^{3/2}cos^3(\theta/2))}$$

Then it should be a relatively simple matter of integrating sec³ of something. There's a wikepedia page on this integral.

 

[GreenPrint]

ya the only problem is that i don't think there is an error in my work i have checked over it a lot, it's not as long as it seems it's just that I showed each step and my reasoning and any formulas I used, I included the reduction formula for integrating secant
I got it down to
12 integral sec^3(u) du

similar to what you got
6*sqrt(2) integral sec^3(x)
interesting enough when i enter this into my calculator with limits i get divide by zero error :O when i try to put in what you got 12*sqrt(2)*integral[0,pi/2] sec^3(x)dx
and wolfram alpha
http://www.wolframalpha.com/input/?...t(2)*integral[0,pi/2]+sec^3(x)dx&incTime=true
couldn't give an approximation or exact answer
hmm...

 

[GreenPrint]

it told me that the correct answer is
6*(sqrt(2)+ln(1+sqrt(2))
yay i got it right and found my error yippeeee