What Is the Linear Acceleration of the Hoop in a Pulley System?

[cp255]

Homework Statement

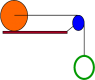
An green hoop with mass mh = 2.6 kg and radius Rh = 0.12 m hangs from a string that goes over a blue solid disk pulley with mass md = 2.3 kg and radius Rd = 0.09 m. The other end of the string is attached to a massless axel through the center of an orange sphere on a flat horizontal surface that rolls without slipping and has mass ms = 3.3 kg and radius Rs = 0.23 m. The system is released from rest.

What is magnitude of the linear acceleration of the hoop?

Homework Equations

T = Ia
F=ma
I_sphere = 0.0698
I_disc = 0.00932

The Attempt at a Solution

F_1 = 9.81 * mass_of_hoop = 25.506 N
F_2 = the force exerted on the sphere.
a = the acceleration of the sphere and hoop

a = ((F_1 - F_2)r_disc^2) / I_disc
a = (F_2 * r_sphere ^ 2)/I_sphere

The first equation tells is the acceleration of the rope over the pully. The second one is the acceleration of the sphere. The resultant acceleration is greater than 9.81 so I know it is wrong. I tried changing to second equation to a = ((F_2 - (m_sphere * a)) * r_sphere ^ 2)/I_sphere but that is also wrong.

 

[altamashghazi]

use rxf=i.α for torque and Newtons equation for force and accln.

 

[cp255]

What is rx.

 

[cp255]

I got it. I needed to also account for the mass of the hoop in the second equation.