What is the Mass Range M/m for the Ring to Rise as the Beads Fall?

[Karol]

Homework Statement

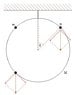
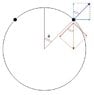
A smooth hoop of mass M with 2 beads of mass m each hangs from the ceiling. at t=0 the beads are released from the top and they start sliding down.
What is the mass range M/m for the ring to rise as the beads fall.

Homework Equations

Friction force: $f=mg\mu$

The Attempt at a Solution

I don't see how the normal forces can raise the ring. when on the upper or lower half of the ring the normal forces pull down the ring. and that's before i consider linear momentum or anything else.

 

[Dr. Courtney]

Since the beads are constrained to a circle, they are undergoing circular motion. Thus, the the hoop is always applying a component of force toward the center of the circle. By Newton's third, the beads are always applying a component of force away from the center of the circle. Thus, when the beads are on the top half of the circle there can be a net upward force.

 

[TSny]

At the beginning of the motion, the normal force from the hoop acting on a bead is radially outward. Thus, the force of the bead on the hoop is radially inward.

However, as the bead continues to slide there will be a special point where the normal force between the bead and the hoop goes to zero while the bead is still on the upper half of the hoop. (Recall the problem of someone sliding down a hemispherical dome.)

What is the direction of the normal force on the bead once the bead is past this special point?

 

[Karol]

To find the velocity conservation of energy from the top as reference. θ is measured from the vertical as in the new drawing:
$$mgR=\frac{1}{2}mv^2+gmR\cos\theta\;\rightarrow v^2=2gR(1-\cos\theta)$$
The force is the subtraction of the component of gravity from the centripetal force:
$$F=m\frac{v^2}{R}\cos\theta-mg\cos\theta=mg[\cos\theta(1-2\cos\theta)]=mg(\cos\theta-2\cos^2\theta)$$
$$F'=mg(\sin\theta-4\cos\theta)=0\;\rightarrow \tan\theta=4$$
$$\cos\theta=\frac{1}{\sqrt{1+\tan^2\theta}}\;\rightarrow \cos\theta=\frac{1}{\sqrt{1+4^2}}=0.242$$
The velocity at this θ is $v^2=2gR\left( 1-\frac{1}{\sqrt{17}} \right)$
The force at that θ:
$$F=2mg\left( 1-\frac{1}{\sqrt{17}} \right)\frac{1}{\sqrt{17}}-mg\frac{1}{\sqrt{17}}\geqslant M\;\rightarrow \frac{M}{m}\leqslant 1.22$$

 

[Nathanael]

The force is the subtraction of the component of gravity from the centripetal force:
$$F=m\frac{v^2}{R}\cos\theta-mg\cos\theta$$

Why did you use $m\frac{v^2}{R}\cos\theta$ as the centripetal force?

Also on your last line you don't want to use the full normal force, just (twice) the vertical component.

Edit:
In fact you don't even want to maximize the normal force like you did, you just want to maximize the vertical component.

 

[Karol]

$$F=m\frac{v^2}{R}-mg\cos\theta=mg(2-3\cos\theta)$$
$$F_y=F\cos\theta=mg(2\cos\theta-3\cos^2\theta)$$
$$F'_y=mg(-\sin\theta-6\cos\theta)\;\rightarrow\;\tan\theta=-6 \;\rightarrow\;\cos\theta=\frac{1}{\sqrt{37}}$$
$$2F_y=2mg\frac{1}{\sqrt{37}}\left( 2-\frac{3}{\sqrt{37}} \right)\geqslant M\;\rightarrow\; \frac{M}{m}5\leqslant 5.13$$

 

[Nathanael]

$$F'_y=mg(-\sin\theta-6\cos\theta)$$

This isn't right

 

[haruspex]

Thus, the the hoop is always applying a component of force toward the center of the circle.

Only when the radial component of gravity acting on the beads is insufficient to supply the centripetal force, but clearly that will become true before the beads descend to half way.

 

[Karol]

$$F'_y=mg(\sin\theta-6\cos\theta)\;\rightarrow\;\tan\theta=6 \;\rightarrow\;\cos\theta=\frac{1}{\sqrt{37}}$$
The rest remains unchanged

 

[Nathanael]

$$F'_y=mg(\sin\theta-6\cos\theta)\;\rightarrow\;\tan\theta=6 \;\rightarrow\;\cos\theta=\frac{1}{\sqrt{37}}$$
The rest remains unchanged

No it still isn't right. You're forgetting the chain rule on the second term and you're dropping a constant on the first term.

 

[Karol]

$$F_y=F\cos\theta=mg(2\cos\theta-3\cos^2\theta)$$
$$F'_y=mg[-2\sin\theta+3(2\cdot \cos\theta \cdot \sin\theta)]=2mg\sin\theta(3\cos\theta-1)\;\rightarrow\;\ \cos\theta=\frac{1}{3}$$
$$F_y=F\cos\theta=mg(2\cos\theta-3\cos^2\theta)=mg\cos\theta(2-3\cos\theta)\;\rightarrow\; F_y=\frac{2}{3}mg$$
$$\frac{2}{3}mg \geqslant Mg\;\rightarrow\; \frac{M}{m}\leqslant \frac{2}{3}$$

 

[haruspex]

$$F_y=F\cos\theta=mg(2\cos\theta-3\cos^2\theta)$$
$$F'_y=mg[-2\sin\theta+3(2\cdot \cos\theta \cdot \sin\theta)]=2mg\sin\theta(3\cos\theta-1)\;\rightarrow\;\ \cos\theta=\frac{1}{3}$$
$$F_y=F\cos\theta=mg(2\cos\theta-3\cos^2\theta)=mg\cos\theta(2-3\cos\theta)\;\rightarrow\; F_y=\frac{2}{3}mg$$
$$\frac{2}{3}mg \geqslant Mg\;\rightarrow\; \frac{M}{m}\leqslant \frac{2}{3}$$

Looks right, except... have you allowed for the fact there are two beads?

 

[Karol]

$$2\cdot \frac{2}{3}mg \geqslant Mg\;\rightarrow\; \frac{M}{m}\leqslant \frac{4}{3}$$

 

[haruspex]

$$2\cdot \frac{2}{3}mg \geqslant Mg\;\rightarrow\; \frac{M}{m}\leqslant \frac{4}{3}$$

On second thoughts, it looks like you introduced a factor of 2 in the preceding line.
Where you wrote $F_y=\frac 23 mg$, shouldn't that have been $\frac 13$?

 

[Karol]

Yes you are right, i already introduced the factor of 2 in $F_y=\frac 23 mg$