What is the net torque on a wheel with given dimensions and direction?

AI Thread Summary
The discussion focuses on calculating the net torque on a wheel with specified dimensions and direction, using the formula torque = force x distance. Participants calculate individual torques, noting that the 30-degree angle in the problem may be misleading. The net torque is ultimately determined to be -2.96, indicating a clockwise rotation. Clarification is provided that the 12 N force acts tangentially to the circle of radius a. The conversation highlights the importance of understanding the role of angles in torque calculations.
aaronb
Messages
22
Reaction score
0

Homework Statement


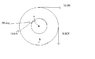
find the net torque on the wheel about the axle through O, taking a = 7.00cm and b = 20.00cm. Assume the positive direction is counterclockwise


Homework Equations


torque = force x distance
torque = force x (radius x sin(phi))


The Attempt at a Solution


10.0 x .2m = -2 (because it's moving clockwise)
9.00 x .2m = -1.8
.07 x 12 x sin(30) = .42

net torque = -3.38 (this is off by 10%-100%)
 

Attachments

  • physicshw10and11prob7.jpg
    physicshw10and11prob7.jpg
    12 KB · Views: 452
Physics news on Phys.org
I don't understand what the 30 degree angle represents.
 
Me niether, do you think it was put there to confuse?
 
aaronb said:
Me niether, do you think it was put there to confuse?
Beats me. It looks like the 12 N force is tangential to the circle of radius a. Is that the case?
 
It is there to confuse. The net torque turned out to be -2.96 so the 12N force is tangential. Thanks for bringing that up to attention
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Force on a rotating wheel/disc
Replies
25
Views
2K
Torque on a Circular Current Loop under a Misaligned Magnetic Field
Replies
1
Views
938
Calculating Net Torque on Wheel Axle
Replies
7
Views
4K
Finding the net torque about the axle?
Replies
3
Views
5K
Calculating Net Torque for an Inclined Wheel: A Problem in Applied Physics
Replies
4
Views
2K
Force exerted on counter-rotating wheels by a tennis ball
Replies
44
Views
6K
Understanding cross product and direction of torque
Replies
4
Views
2K
What is the total torque of that system?
Replies
28
Views
3K
Find the tension in the cable and reactive forces at ground
Replies
4
Views
5K
How Do You Calculate Torque on a Wrench?
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top