tiffany09
- 3
- 0
1. Homework Statement
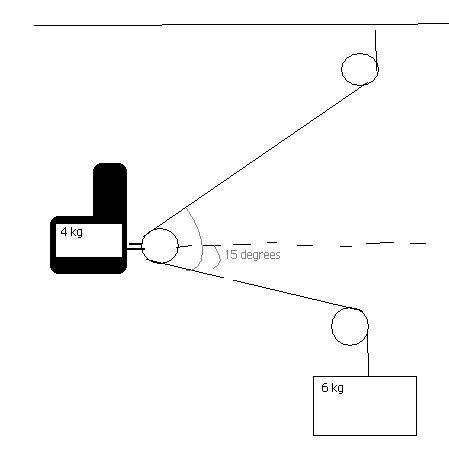
Can you see the picture?
"An accident victim with a broken leg is being placed in traction. The patient wears a special boot with a pulley attached to the sole. The foot and boot together have a mass of 4 kg, and the octor has decided to hang a 6 kg mass from the rope. The boot is held suspended by the ropes and does not touch the bed.
a) Determine the amount of tension in the rope by using Newton's laws to analyze the hanging mass.
b) The net traction force needs to pull straight out on the leg. What is the proper angle (theta) for the upper rope?
c. what is the net traction force pulling on the leg?
hint: if the pulleys are frictionless, which we will assume, the tension in the rope is constant from one end to the other"
2. Homework Equations
F= ma
3. The Attempt at a Solution
The 6kg hanging mass is pulling on the rope with 58.8 N right? but then how does the pulley and angles affect everything? the answer to A is 58.8 N right? Is that tension the same in all parts of the rope? That's what the hint is telling us right?
For b and c, i don't even understand what it's asking. What's a net traction force?
so since we know the tension of the string is 58.8 N, that means that the hypotenuse to the triangle with the 15 degree angle is 58.8 too right? The hypotenuse being the length of rope between the two pullies?
From that can we say the lengths of the sides of that triangle is 58.8sin15 (15.219) and 58.8cos15(65.796)? but then what do you do with that information? I still don't get b & c
Can you see the picture?
"An accident victim with a broken leg is being placed in traction. The patient wears a special boot with a pulley attached to the sole. The foot and boot together have a mass of 4 kg, and the octor has decided to hang a 6 kg mass from the rope. The boot is held suspended by the ropes and does not touch the bed.
a) Determine the amount of tension in the rope by using Newton's laws to analyze the hanging mass.
b) The net traction force needs to pull straight out on the leg. What is the proper angle (theta) for the upper rope?
c. what is the net traction force pulling on the leg?
hint: if the pulleys are frictionless, which we will assume, the tension in the rope is constant from one end to the other"
2. Homework Equations
F= ma
3. The Attempt at a Solution
The 6kg hanging mass is pulling on the rope with 58.8 N right? but then how does the pulley and angles affect everything? the answer to A is 58.8 N right? Is that tension the same in all parts of the rope? That's what the hint is telling us right?
For b and c, i don't even understand what it's asking. What's a net traction force?
so since we know the tension of the string is 58.8 N, that means that the hypotenuse to the triangle with the 15 degree angle is 58.8 too right? The hypotenuse being the length of rope between the two pullies?
From that can we say the lengths of the sides of that triangle is 58.8sin15 (15.219) and 58.8cos15(65.796)? but then what do you do with that information? I still don't get b & c