OierL
- 5
- 0
Homework Statement
In a distant galaxy, a planet orbits its sun at a distance of
Select one:
a.
b.
c.
d.
e.
Homework Equations
T^2=constant * r^3
The Attempt at a Solution
First of all I compute the constant whit the values of the first planet:
(108)^2 = const. * (1'8*10^12)^3 → const= 2*10^-33
Then, I compute the period of the second planet:
T^2 = 2*10^-33 * (9*10^11)^3 → T = √1458 = 38,18 s
This solution doesn't apear in the results I have to choose. What do I have wrong?
Thank you!
Attachments
-
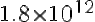 c28fb096237b0a04a15c64e37a292086.gif561 bytes · Views: 560
c28fb096237b0a04a15c64e37a292086.gif561 bytes · Views: 560 -
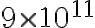 6b8c23b8fdf999e3d16717c8daf58b5e.gif463 bytes · Views: 530
6b8c23b8fdf999e3d16717c8daf58b5e.gif463 bytes · Views: 530 -
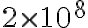 55c2bc2f030e754241487b390145364b.gif489 bytes · Views: 321
55c2bc2f030e754241487b390145364b.gif489 bytes · Views: 321 -
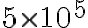 b1558216fac73da8cf7be349fc9c0524.gif460 bytes · Views: 324
b1558216fac73da8cf7be349fc9c0524.gif460 bytes · Views: 324 -
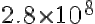 aaaf30018536b0436cdd4a744f488597.gif584 bytes · Views: 311
aaaf30018536b0436cdd4a744f488597.gif584 bytes · Views: 311 -
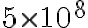 605809b649a0376f8fa4b8c28d33f15f.gif481 bytes · Views: 307
605809b649a0376f8fa4b8c28d33f15f.gif481 bytes · Views: 307 -
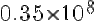 6f428d14e6b8e2ae0744043ee5d58576.gif659 bytes · Views: 315
6f428d14e6b8e2ae0744043ee5d58576.gif659 bytes · Views: 315