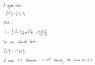What is the Potential of Quintessence Without Astronomical Units?

[shadi_s10]

Dear all,

I am reading some texts about quintessence. As you one of the best textbooks for cosmology is Weinberg's. in page 90 of his book he states that if we consider astronomical units we can see that a good quintessence potential is

V(\phi)= (M^(4+alpha)) * phi ^(-alpha)

and M has the dimention of mass.

Can anyone tell me if we do not work in that unit (I mean we do not consider h=c=1) what would exactly the potential be?
please help!
I really need to know this...

 

[grey_earl]

Take your complete Lagrangian, not just the potential part. The integral of the Lagrangian is the action, which has the same units as \hbar. Then calculate the dimension of \phi from the kinetic term, and from this infer the factors of c and \hbar you need to make the potential the same dimension as the kinetic term. Shouldn't be that hard, I suppose ...

(Caveat: The normalization of \phi is ambigous, but this doesn't matter in the end)

 

[shadi_s10]

Take your complete Lagrangian, not just the potential part. The integral of the Lagrangian is the action, which has the same units as \hbar. Then calculate the dimension of \phi from the kinetic term, and from this infer the factors of c and \hbar you need to make the potential the same dimension as the kinetic term. Shouldn't be that hard, I suppose ...

(Caveat: The normalization of \phi is ambigous, but this doesn't matter in the end)

Dear friend,
thanks a lot for helping me.
I have tried this method befire but unfortunately there is a problem.
I attached my computations in the file below.
I would appreciate it if you could read it.
Thanks for your help.

shadi

 

[grey_earl]

Note that the equation should be dimensionally correct independent of \alpha. So, from your potential V(\phi) = M^{4+\alpha} \phi^{-\alpha}, M must have the same dimensions as \phi.

 

[shadi_s10]

Note that the equation should be dimensionally correct independent of \alpha. So, from your potential V(\phi) = M^{4+\alpha} \phi^{-\alpha}, M must have the same dimensions as \phi.

I agree that V should be independent of alpha. But if M has the same dimensions as \phi , then the dimension of V would be like \phi^{4}. Why do you say that?

 

[grey_earl]

\alpha can be any number. If your final expression depended on \alpha, the dimension of your action would depend on \alpha, but this cannot be. Also, you have made a mistake in your first step: I said the dimension of the action is the same as the dimension of \hbar, so since the action is the space-time integral of the Lagrangian, the Lagrangian has dimensions of
[\hbar] \mathrm{m}^{-3} \mathrm{s}^{-1}, which is (since [\hbar] = [energy] \mathrm) equal to [energy] \mathrm{m}^{-3}.

Also, you forgot that there could be a factor containing c and \hbar multiplying the kinetic term. So you should reason as follows:

- M must have the same units as \phi, since otherwise the dimension of the action wouldn't be independent of \alpha
- The dimensions of the potential term are therefore dimensions of some unknown function of c and \hbar, times the unit of \phi^4, so
[V] = (m/s)^a (kg m²/s)^b [φ]⁴ = kg/m/s² (since that's the dimension of the Lagrangian)
- The dimensions of the kinetic term are analogously
[T] = (m/s)^c (kg m²/s)^d (1/m [φ])² = kg/m/s²

Therefore, from the kinetic term we get [φ]² = kg m/s² (s/m)^c (s/kg/m²)^d, and inserting this into the potential term we have
(m/s)^a (kg m²/s)^b kg m³/s² (s/m)^(2c) (s/kg/m²)^(2d) = 1
For the kilograms we get kg^b kg (1/kg)^(2d) = 1, so b+1-2d=0.
For the seconds we get (1/s)^a (1/s)^b 1/s² s^(2c) s^(2d) = 1, so -a-b-2+2c+2d=0.
For the meters we get m^a (m²)^b m³ (1/m)^2c (1/m²)^(2d) = 1, so a+2b-2c-4d=0.
Now you need to solve those three equations. Combining the second and third, I get

b-2d=-1
b-2d=2

This is clearly inconsistent, so unless I made an error in my calculation (which may be), you quintessence potential is either nonsense, or you have to put in an extra factor of c^\alpha or c^{2\alpha} or \hbar^\alpha or the like in your potential to account for the \alpha dependence. Then the dimension of V times this factor should be independent of \alpha. I think you can do the calculation from there on yourself, you may need to try a bit.

 

[shadi_s10]

Dear friend,

Thanks for your help.
I agree that V's dimension should be M^4. you're completely right about it.
But take a look at my note .
I don't think V's dimention is exactly L's (the energy).

 

[grey_earl]

Sorry for the confusion! When I say Lagrangian, I mean Lagrangian density, that's standard parlor in the theoretical physics community.

So in your notation
S = \int L \mathrm{d}t = \int [ (\partial^\mu \phi) (\partial_\mu \phi) - V ] \sqrt{-g} \mathrm{d}^4 x.
When I say Lagrangian I then mean only the part inside square brackets, [ (\partial^\mu \phi) (\partial_\mu \phi) - V ], and this doesn't have dimensions of energy. But of course, the space integral of this, what you say - rightly! - is the Lagrangian, has dimensions of energy.