What is the Ratio of Thicknesses for a Beam Splitting on a Stationary Plate?

[mathmari]

Hello!

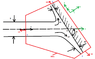
A two-dimensional beam of thickness S and velocity c (evenly distributed at the thickness) falls in stationary plate and get separated. Calculate the ratio of thicknesses S1/S2 as a function of the angle φ.

(see attachment)In my notes there is this solution:

Continuity equation:

Let c₁, c₂ the velocities of the sections 1, 2

$$0: \overrightarrow{u}=c\hat{e} \ \ , \ \ \overrightarrow{n}_0=-\hat{e}=-(-\sin \phi \hat{i}+\cos \phi \hat{j}) \Rightarrow \overrightarrow{u} \cdot \overrightarrow{n}_0=-c \\ 1: \overrightarrow{u}=c_1 \overrightarrow{n}_1=c_1 \hat{i} \ \ , \ \ \overrightarrow{n}_1=\hat{i} \Rightarrow \overrightarrow{u} \cdot \overrightarrow{n}_1=c_1 \\ 2: \overrightarrow{u}=c_2 \overrightarrow{n}_2=-c_2\hat{i} \ \ , \ \ \overrightarrow{n}_2=-\hat{i} \Rightarrow \overrightarrow{u} \cdot \overrightarrow{n}_2=c_2$$

$$\int_{\partial{W_1}}\overrightarrow{u} \cdot \overrightarrow{n}dA=0 \Rightarrow -c \cdot (S \cdot 1)+c_1 \cdot (S_1 \cdot 1)+c_2 \cdot (S_2 \cdot 1)=0 \Rightarrow cS=c_1S+c_2S_2 \ \ \ \ \ (1) $$

Conservation of energ $\Rightarrow $ Bernoulli equation

$$\frac{1}{2}|\overrightarrow{u}|^2+\frac{p}{\rho_0}=\text{ constant along a stremline }$$

$$0 \rightarrow 1 : \frac{1}{2}c^2+\frac{p_a}{\\rho_0}=\frac{1}{2}c_1^2+\frac{p_a}{\rho_0} \Rightarrow c_1=c \\ 0 \rightarrow 2 : \frac{1}{2}c^2+\frac{p_a}{\\rho_0}=\frac{1}{2}c_2^2+\frac{p_a}{\rho_0} \Rightarrow c_2=c \\ \Rightarrow c_1=c_2=c \ \ \ \ \ (2)$$

$$(1) \wedge (2) \Rightarrow S=S_1+S_2 \ \ \ \ \ (3)$$

$$\overrightarrow{F}_{W_0}=-\int_{\partial_{W_1}}p \overrightarrow{n} dA-\int_{\partial{W_1}}\rho \overrightarrow{u} (\overrightarrow{u} \cdot \overrightarrow{n})dA$$

$$\int_{\partial_{W_1}}p \overrightarrow{n} dA=p_a \int_{\partial{W_1}}\overrightarrow{n}dA=0$$

$$\int_{\partial{W_1}}\rho \overrightarrow{u} (\overrightarrow{u} \cdot \overrightarrow{n})dA=\rho_0 (c \hat{e}(-c)S+c_1 \hat{i}c_1S_1+(-c_2 \hat{i})c_2S_2)=(\rho_0c^2S\cos \phi +\rho_0 c_1^2S_1-\rho_0c_2^2S_2)\hat{i}-\rho c^2S\sin \phi \hat{j}=-\overrightarrow{F}_{W_0}$$

$$F_{W_0, x}=-\rho_0c^2(S\cos \phi +S_1-S_2) \ \ \ \ \ (4a) \\ F_{W_0, y}=\rho c^2 S \sin \phi \ \ \ \ \ (4b)$$

Since the fluid is ideal we have that $$F_{W_0, x}=0 \Rightarrow S_2-S_1=S \cos \phi \ \ \ \ \ (5)$$

$$(3) \wedge (5) \Rightarrow \\S_1=\frac{S}{2}(1+\cos \phi) \\ S_2=\frac{S}{2}(1-\cos \phi) \\ \Rightarrow \frac{S_2}{S_1}=\frac{1-\cos \phi}{1+\cos \phi}$$
Could you explain to me the general idea of the solution? I haven't really understood that...Every time when we have such an exercise do we have to use the continuity equation and the Bernoulli equation?

Also could you explain to me why the following equality stand?

$$\int_{\partial{W_1}}\rho \overrightarrow{u} (\overrightarrow{u} \cdot \overrightarrow{n})dA=\rho_0 (c \hat{e}(-c)S+c_1 \hat{i}c_1S_1+(-c_2 \hat{i})c_2S_2)$$

 

[Chestermiller]

You are learning how to apply macroscopic balances to solve certain types of fluid mechanics problems (that are amenable to this type of approach). Which part of the approach don't you understand: (a) continuity equation, (b) conservation of mechanical energy (Bernoulli) equation, or (c) macroscopic momentum balance equation? You seem to be indicating that you are not comfortable with the application of the macroscopic momentum balance equation, correct?

Chet

 

[mfb]

There seems to be a sign or labeling error. A small ϕ (and therefore large cos ϕ) should make S2 large and S1 small, not the opposite.