Optical What is the Relationship between Angles and....pixels?

[Justice Hunter]

Wasn't really sure how to ask this question since it's kind of niche.

I have 3 cameras, which have the property that they occupy no physical space, and have no lens. They are defined only by the angle of their view.

Now these cameras capture a certain field and take an image. The cameras will always creates an image that's 1280 pixels in length, and 720 pixels in height. The other two cameras Left and Right, are rotated along the center cameras axis by any arbitrary amount, and create an elongated image of the center camera. So when the Left and Right cameras are placed and then rotated at the same Angle of View as the center camera, the amount of pixels the field of view extends to is 3x1280, which would be 3840. Below is an illustration that reflects this.

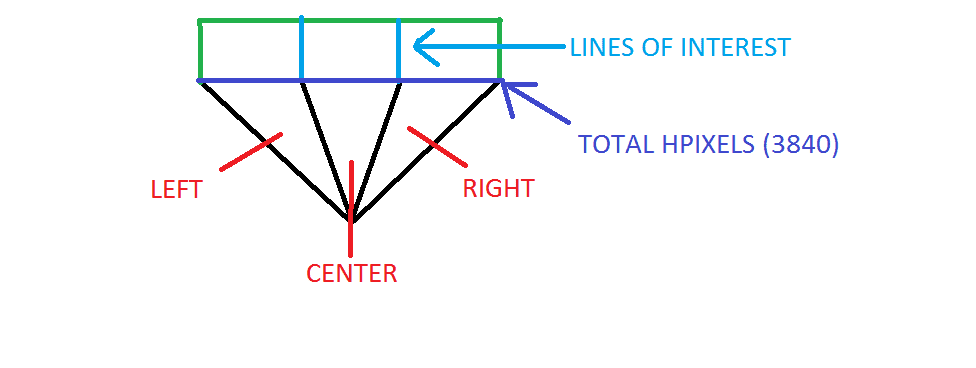
Additionally, if the Left and Right cameras are placed at 0 rotation from the center camera, the minimum Field of View is 1280pixels.

So that's the setup. Now the issue arises when i want to find out the relationship between the light blue lines (Lines of Interest) and the angle of view of the L and R cameras.. Essentially, as the angle of the Left and Right cameras increase or decrease, while the center cameras angle remains the same, the position of the Lines of Interest also changes, as well as the total amount of the field of view (The purple line).

My problem is finding out the overlap in terms of pixels, when the angle of view of the Left and Right cameras change. So for example if the L and R cameras are rotated 10degrees from the center camera, the position of those blue lines changes to some number between 0 and 1280 (0 being no change in angle, and 1280 being a change in angle that's equal to the angle of the center camera.

I searched online for anything remotly close to this, but many of the things i found online had to deal with cameras that took up real space, which involved real physics behaviour about light and lens's, which is not what I'm looking for. I'm looking for a much more mathematical explanation which are mostly about relationships to triangles.

 

[Charles Link]

Generally a camera needs to have a lens, and if the object is far away, the detector array is in the focal plane of the lens. There is a pinhole type camera that is an exception to this, but otherwise, an array of pixels as a detector is not going to be able to image anything.

 

[Borek]

Apart from the real life thing that Charles addresed above, sounds to me like all you need to solve this type of a problem is some basic geometry. There are some triangles and angles involved, but you shouldn't need anything more complicated than a basic trigonometry to calculate everything.

 

[hutchphd]

I agree with the the previous comments. For your analysis, any camera can be considered just a "pinhole" camera. The rest is plane geometry. I don't really understand, from your description, the exact question you have.

 

[Justice Hunter]

Thanks guys for the replies, but i ended up finding the answer to my question while attempting to write my comment further articulating the problem. The above is described by a Proportion:

LOI/Hpixel = AOS/TAoV

Where LOI is the line of interest (our variable)
Hpixel is the fixed number of horizontal pixels
AOS is the angle of separation from the center camera ∠[(L+R)-C]
TAoV is the angle of the center camera, plus the angles of separation of L and R ∠[L+C+R]

So, for example : LOI/1920 = 20/50. If my center camera (assumes all cameras have same angle of view) have an angle of 30, then the total angle of two cameras tilted 10 degrees away from the center gives it a total of 50 degrees, and sets the AOS to 20 in the numerator. The LOI will always spit out a number between 0 and 1280 (In this case it's 768), which was surprising to me, but it's what confirms that the relationship is true.

I know the answer could be articulated a bit better, but for now this solves my current problem, if anyone wants to clean up that answer that would be nice.

Thanks again.

 

[Baluncore]

We view our spherical world through a lens, by projecting it onto our spherical retinas.

There is a problem with your model of the camera. The view is being considered in spherical coordinates, but the rectangular image is formed on the plane surface of an image sensor.

The edges of adjacent images will not match unless you distort the Cartesian images to make the directional lines of longitude vertical.

 

[.Scott]

As I understand it, you have three pinhole cameras sharing the same pinhole.
So the only different among those cameras are their image planes.
Your two lines of interest land on a plane that we will call the subject plane.

Let's say that the all three cameras have a view that extends 30 degrees to the left and right of the center-of-view axis - a total 60-degree view.

We will also say that the center camera and just barely includes your two lines of interest. It will divide the space between those line into 1280 parts - and because the subject plane is parallel to the center cameras image plane, those pixels will be evenly spaced along the subject plane.

Now your right and left cameras are not looking directly at the subject plane. You do not show their image planes, but normally the image plane is perpendicular to a ray extending from the focal point (pin hole) to the center of the camera view - and so I will assume that to be the case.

Let's say that each of them is rotated 30 degrees to the side (relative to the center camera). So they will have a view that runs from 0 to 60 degrees or 0 to -60 degrees.

Since each side camera is catching half the frame of the center camera, it will have have 640 pixels of overlap with that center camera. But be careful. Even though there are 640 pixels of overlap, those 640 center camera pixels and 640 side camera pixels are not distributed across the subject plane in the same way. Also, the width of center wall captured by the center camera will be less that that captured by either side camera. This is especially true when the side cameras are rotated far enough for them to catch the subject plane horizon in their view. When this happens, the amount of subject plane surface area captured by each side camera becomes infinite.