What is the required piston force for a crane boom with specific dimensions?

[kraub]

TL;DR Summary

Calculating rotation force

Hello,

I have 2 pics about my case, I has designed crane boom and the problem has occurred when i came this point. As you see the pics, i want to find piston force. Could you help me about this ? (Dimensions=mm )

 

[Baluncore]

Welcome to PF.
A very quick estimate of piston force due to load is;
0.15 kN * ( 5500 / 500 ) / Sin( 12 deg) = 7.93 kN
Remember to add the weight of the jib to the problem.

 

[FEAnalyst]

Welcome to PF.
A very quick estimate of piston force due to load is;
0.15 kN * ( 5500 / 500 ) / Sin( 12 deg) = 7.93 kN
Remember to add the weight of the jib to the problem.

Could you share a simple scheme or derivation ? I'm curious how you got to this equation.

 

[Baluncore]

Could you share a simple scheme or derivation ?
I'm curious how you got to this equation.

The OP waited for 12 hours before getting any reply.
I think you should stake your bid before asking me to explain or justify mine.

 

[FEAnalyst]

The OP waited for 12 hours before getting any reply.
I think you should stake your bid before asking me to explain or justify mine.

If I had an idea how to calculate this force I would definitely share it. But I don’t know how to do and since I’m curious about this topic, I’m asking for additional explanation regarding your solution.

 

[Baluncore]

I’m asking for additional explanation regarding your solution.

There is insufficient information to be certain of any precise numerical result.

We do not need to chase the OP away with a shower of questions.
We just need an approximate answer, ignoring wind forces.

A crane boom and jib can be manipulated into many orientations. This is a student's concept, not an optimised design. It is shown in what is a "close to worst case position”. The following four steps appeared fundamental to my first approximation.

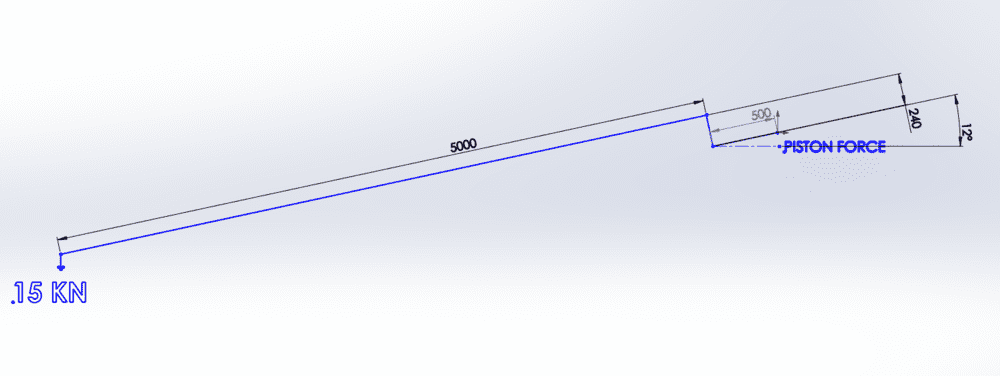
1. The 240 mm sidestep in the jib is irrelevant in the first analysis, so I ignore it.

2. The load is 150 N, so the crane can be a very light weight structure, probably a composite tube.

3. The jib is a lever that is 5500 mm long, with hydraulic force applied at 500 mm. That provides the ( 5500 / 500 ) term.

4. The hydraulic cylinder applies a force between the boom and jib. Model the elbow as two links with a 180° sweep. Then at 90° (between jib and cylinder) the cylinder will apply force directly with factor of 1.0; At 0° and 180° the points of attachment will be in line so the force will be infinite. The appropriate first order approximation is therefore the reciprocal of the sine function.

That explains the three terms of my approximation. F = 0.15 kN * ( 5500 / 500 ) / Sin( 12° ).

 

[kraub]

Hello everyone,

Thanks your ideas and solutions. I think that mistake, when i give you this basic diagram . Because i separated the system with chasis. But the piston force is providing stabilizing in the system, in this case i have to draw like this picture. The line that new drawing is 1600 mm. My opinion that moment of this point take by there. What do you think about it ? Is that true way ? Thank you again your ideas and interests.

 

[Baluncore]

I do not understand.
Problem with translation.
Which line is 1600 mm?

 

[kraub]

I do not understand.
Problem with translation.
Which line is 1600 mm?

 

[Baluncore]

Insufficient information.
To solve the triangle you must specify three lengths between pins, or two lengths and one angle.

What is the distance along the boom from the jib hinge pin to the cylinder end pin on the boom?

You have not made it clear if the 1600 mm is the extended length of the ram from eye to eye measured diagonally, or if it is the separation of the cylinder eyes measured horizontally?

 

[kraub]

The dimensions of triangle that 500,1200 and 1600 mm. The 1600 mm of cylinder is extended dimension. It is stabilization position.

 

[Baluncore]

The triangle has sides: a = 5; b = 12; c = 16.
The internal angles are: A = 12.429°; B = 31.102°; C =136.469°
The angle between the jib and the horizontal (boom) is therefore; 180° - 136.469° = 43.531°

That is much steeper than your drawing so I assume there is something wrong with your numbers, diagram or my computation. Can you please solve for the angles of the triangle.

 

[kraub]

You miss something there, angle of extended line and boom is different as you see, the drawing is clearly true because it is drew by computer programming, even i am asking about way of solution that share of force and moment.

 

[Tom.G]

Measuring the image in a graphics program, using 1600 as the 'standard ruler', gives these results:

The Right-Most arm is Horizontal, its top edge measured as 0.0°

Pivot to left end of Cylinder: 364.4
Pivot to right end of Cylinder 1229
Cylinder Extension: 1600
Angle of Boom to Horiz.: 12.1° Counter Clock Wise
Angle of Cylinder to Horiz: 3.3° CCW
Length of Blue line on Boom: 3688

These are point-to-point measurements, not horizontal projections.

Cheers,
Tom

 

[Baluncore]

You miss something there, angle of extended line and boom is different as you see, the drawing is clearly true because it is drew by computer programming, even i am asking about way of solution that share of force and moment.

I do not trust your computer.
When the triangle has dimensions 500, 1200, 1600 mm, what is the angle between the horizontal boom and the hinged jib?
I believe it is 43.531°

 

[Baluncore]

When the jib hangs vertical there is zero moment due to supported end load plus jib weight.
The jib has a maximum moment due to weight and end load when the jib is horizontal.
At that point, the optimum angle between jib pins and hydraulic cylinder is 90°.
A fundamental problem with your design as that the angle is 0°, when it needs to be 90°.

Another limitation is the hydraulic cylinder pin attachment points.
The length of a standard hydraulic ram cannot change by a factor of two.
1200–500 = 700; 1200+500 = 1700; That full range is impossible.
There must be physical stops to prevent the piston hitting the internal ends of the cylinder.

 

[Dr.D]

The length of a standard hydraulic ram cannot change by a factor of two.
1200–500 = 700; 1200+500 = 1700; That full range is impossible.

Actually, this is possible with a telescoping cylinder, but that is not very common.

 

[Baluncore]

Attached is cylinder force table and BASIC code used for computation.

 

[Baluncore]

The dimensions of triangle that 500,1200 and 1600 mm. The 1600 mm of cylinder is extended dimension. It is stabilization position.

Focusing in on my computed data shows that, when the jib dips at an angle of 43.5°; the cylinder will have a length of 1600 mm; and the hydraulic force required will be 1.445 kN.

Actually, this is possible with a telescoping cylinder, but that is not very common.

A telescoping cylinder cannot be hydraulically retracted because it has no piston. It must be closed by the weight of the load.
A cylinder having a pintle mount, somewhere along the cylinder rather than an eye at the end, does make it possible to retract by more than a factor of two between the mountings.