You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is the solution to the non-linear device problem?
- Thread starter jegues
- Start date
-
- Tags
- Device Non-linear
AI Thread Summary
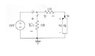
The discussion centers on solving a non-linear device problem using Kirchhoff's voltage law (KVL). The user initially struggles with the equation involving voltage and current ratios, specifically \(\frac{1+v_Q/i_Q}{2+v_Q/i_Q} = 10\). They clarify that the 1-ohm resistor is in parallel with a 10V source, leading to a voltage drop calculation that includes the current through another resistor. After reevaluating their approach, they recognize the error in equating resistance to voltage and arrive at a solution of \(V_{q} = 2V\). The conversation emphasizes the importance of correctly applying KVL and understanding the relationships between voltage and resistance in circuit analysis.
Physics news on Phys.org
vela
Staff Emeritus
Science Advisor
Homework Helper
- 16,203
- 2,854
Could you explain your reasoning to get the equation
\frac{1+v_Q/i_Q}{2+v_Q/i_Q} = 10
I don't see how you're applying Kirchoff's voltage law to get that.
\frac{1+v_Q/i_Q}{2+v_Q/i_Q} = 10
I don't see how you're applying Kirchoff's voltage law to get that.
wwshr87
- 59
- 0
You know the 1 ohm resistor is in parallel with the 10V source, therefore the voltage across it is 10V. Now we can subtract from the 10V the drop across the other 1 ohm resistor which is 1*Iq, and subtract Vq. 10 - 1*Iq - Vq=0, we can plug in for Iq which is Vq^2+2*Vq. Solve for Vq, you'll obtain a positive and negative value but only the positive makes sense because of our polarity.
Attachments
Zryn
Gold Member
- 310
- 0
When you combine the circuit resistances, first by adding the two in series, and then by calculating the two in parallel, you get a value of resistance (keep in mind SI units).
In your equations you say this resistance is equal to 10 volts by KVL.
\frac{1+v_Q/i_Q}{2+v_Q/i_Q} = 10
Resistance does not equal voltage.
In your equations you say this resistance is equal to 10 volts by KVL.
\frac{1+v_Q/i_Q}{2+v_Q/i_Q} = 10
Resistance does not equal voltage.
jegues
- 1,085
- 3
Thanks for the responses. I must have been out of it at the time putting resistance equal to voltage lol.
I understand now.
V_{q} = 2V
I understand now.
V_{q} = 2V
Similar threads
- Replies
- 1
- Views
- 1K
- Replies
- 3
- Views
- 2K
- Replies
- 8
- Views
- 2K
Engineering
Noise Floor/Device Temperature Problem
- Replies
- 3
- Views
- 2K
- Replies
- 7
- Views
- 4K
- Replies
- 4
- Views
- 2K
- Replies
- 8
- Views
- 4K
- Replies
- 9
- Views
- 2K
- Replies
- 16
- Views
- 3K
- Replies
- 6
- Views
- 2K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Max water pressure allowable on solar panels
- Started by ethanesh
- Replies: 16
- Engineering and Comp Sci Homework Help
-
Spiral scissor lift statics
- Started by carlcla
- Replies: 4
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 95
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math