littlejon
- 20
- 0
Homework Statement
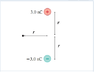
Specify the strength of the electric field. Let r = 7.3cm .
Homework Equations
E1= (k*p)/(r^2+a^2)^3/2
Here k= constant used in Coulomb's law. a= half the length of dipole
p= dipole moment = charge x length of dipole. Charge = 3nC and length of dipole
The Attempt at a Solution
E1= (9E9)(3E-9)/(.146)^2+(.073)^2)^(3/2)= 6207
I got this wrong, but does anyone have any advice on how to solve this?
Attachments
Last edited: