What is the tension in a horizontal rope on an inclined plane with friction?

[ohphysics]

Homework Statement

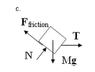
A block of mass M = 2 kg is on a stationary inclined plane inclined with an angle θ = 30°. A horizontal rope is attached to the block and is pulled to the right with tension T. The tension remains horizontal even in the event that the block moves down the plane. The coefficient of static friction between the block and the inclined plane is μs = 0.7 and the coefficient of kinetic friction is μk = 0.5 .

Homework Equations

f=ma

The Attempt at a Solution

I set up the FBD and summed the y component of force but where I get stuck is the tension. Because I know that it has a y component based on my axis but I am not sure how to find it, which is what I am trying to figure out. I am confident that I would understand the rest. for sum of fy i have Nf-mgcos(30)=0 and am not sure how to include the tension. I uploaded the FBD of the box

 

[Orodruin]

What angle does the tension force have to your chosen axes?

 

[ohphysics]

that is what I am confused on. I do not know how to find the angle the tension force has compared to my axes. The axes I started with was x parallel with the incline and normal force parallel with y axis

 

[Orodruin]

How did you find the angle that gravity makes with your axes?

 

[ohphysics]

well because I made x parallel to the incline the change from the gravity vector and gravity's y vector would be the same as the degree of the incline which is 30 degrees

 

[Orodruin]

So with the same reasoning, what is the angle between the tension and the x axis?

Another way of seeing it: What is the angle between gravity and the tension?

 

[ohphysics]

ok I think I see your point. So it would also be a 30 degree angle between tension and the x-axis correct? The way I am thinking about it is if we made the angle of incline 0 what would the tension be. and I'm thinking it would be either 30 or 60 but i'd like a way in which I can tell for sure

 

[BvU]

Not good. The tension is said to remain in the horizontal direction! But it sure has a component along the incline, and also a component perpendicular to the incline... Oro wants to know the angle with those.

 

[ohphysics]

ok so I think that because the axis is tilted 30 degrees down the component along the incline's angle would have to be ftcos30 because the tension is completely horizontal. the component perpendicular to this angle would be ftsin 30. I'm pretty unsure of myself on this concept though

 

[BvU]

But it is perfectly correct. So Nf-mgcos(30)=0 should become what ? (make sure you get the sign right).
I do notice the problem statement lacks a question; do they what the acceleration along the incline ? In that case your x components are more interesting ! Or do they want to know at what T things start moving ?

 

[ohphysics]

the question is What is Tmax the maximum value of T for which the block can be held in place with static friction?

 

[ohphysics]

my gameplan after finding out what the angle was looked like this. the normal force becomes mgcos30 for the block. then I can multiply us to the normal force to find the force of static friction needed to keep the box up. and then I go over to the sum of in the x direction and use that friction in accordance with Ft to find what the max tension is. That looks logically correct to me what do you think? I was also wondering. Since gravity and the force of tension are a 90 degree angle, and gravity's y component has a 30 degree angle, wouldn't that mean the force of tension has a 60 degree angle? or are they not complements because gravitys y component is behind the magnitude of gravity?

Thanks you so much for helping me with this!

 

[BvU]

You've done well so far, now work it out. You have a coordinate system: x downwards along the incline, y upwards perpendicular to the incline. You have a force from gravity, a tension force and a friction force. The latter is pointed upwards along the incline, with a magnitude that follows from the normal force. For the normal force you already had Nf-mgcos(30)=0, but I hope I have managed to convince you that there also is a contribution from T. The balance helps you find the magnitude of the friction force, which is one of the forces in the x-direction. Now the components of the others in the x-direction. At the point where T = Tmax and the thing almost starts to slide they add up to m times a zero acceleration, zero Newton therefore. Done !

 

[ohphysics]

so i started working it out and I realized there is still a problem! first i did sum of f in x direction = 0 and i got mgsin30-Ffriction-Ftcos30=0
the sum in the y direction is Nf-mgcos30+ftsin30=0. Now I believe I need solve for ftsin30 and ftcos30 and then add them as vectors but in order to do that I need to know one or the other. I wanted to solve for the normal force and multiply that by us and sub it into friction but I don't know what ftsin30 is, which means i can't do that. I can't figure out what I am missing here

 

[Orodruin]

mgsin30-Ffriction-Ftcos30=0

According to this, you have put the tension in the same direction as the friction. However, the tension is supposed to act together with gravity to make the box move (see your free body diagram). You can also relate the maximal friction to the normal force Nf. You will then have two equations and two unknowns, which you can solve.

 

[ohphysics]

yes in my work I had +ftcos30 but I just realized that I could easily solve for it now! thanks a lot!

 

[ohphysics]

wait I just realized I have 3 unknowns. Nf, Ftsin30 and Ftcos30. I have been trying to solve for them but can't seem to find a way too. I'm racking my brain trying to figure out how to find Normal force specifically but i don't see a way to manipulate it since we don't know ftsin30

 

[Orodruin]

sin(30^o) and cos(30^o) are well known numbers ... Your unknowns are ft and Nf.

 

[ohphysics]

yes I understand but for fy i have Nf=mgcos30-ftsin30 but since I don't know the force of tension I can't find Nf
and in the x direction forces are mgsin30+ftcos30=ffric. I need the force of friction here to find ft but I need Nf for that which is why I am stuck.

 

[Orodruin]

How would you solve the following system of equations?
y = x + 2
x = 2y - 2

 

[ohphysics]

switch the x and 2y so you have y=x+2 and -2y=-x-2. the x and 2 cancel so you have y=0 plug that back into find x. I still do not understand how I could use a system for this problem though.

 

[Orodruin]

Your two equations are:
$$
N_f =mg \cos 30- f_t \sin30
$$
$$
mg \sin30 + f_t \cos30 =\mu N_f
$$
where $\mu$, $m$ and $g$ are known numbers (and the sine and cos can be computed).

 

[ohphysics]

ok I see. thanks for the help