Suyash Singh
- 168
- 1
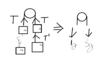
Homework Statement
Homework Equations
g is the acceleration due to gravity
a is the acceleration of system
The Attempt at a Solution
g is the acceleration due to gravity
Force=3(g+a)
Force=6(g-a)
solving both equations,
a=g/3
tension =force=4g
How do i calculate tension in the particular part GH?
and
what does the spring do here?