Cassie1014
I can't figure this out for the life of me .
A large, 2000 pound block is being held by two ropes that were attached to a horizontal beam. The rope on the left made a 30 degree angle, the rope on the right made a 40 degree angle (see image). What is the tension in the left cable?
HINT: Round to the nearest whole number. Do not enter units.
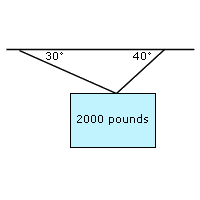
A large, 2000 pound block is being held by two ropes that were attached to a horizontal beam. The rope on the left made a 30 degree angle, the rope on the right made a 40 degree angle (see image). What is the tension in the left cable?
HINT: Round to the nearest whole number. Do not enter units.