andyrk
- 658
- 5
Homework Statement
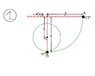
In the given system(see attachment), when the ball of mass 'm' is released from A, it will swing down the dotted arc as shown. A nail is located at a distance 'd' below the point of suspension (O) at M.
(a) What is the tension just before and just after touching the nail?
2. My Attempt
(a)See attachment
Attachment 1 has the situation.
Attachment 2 has the FBD when the sphere is just about to touch the nail.
Attachment 3 has the FBD just after when the sphere has touched the nail.
From attachment 2, equation become as:
Net force towards the centre= Centripetal Force = (mV^{2}_{B})/l = T_{i}-mg
→T_{i}-mg = (mV^^{2}_{B})/l (Equation 1 )
As we have V^^{2}_{B}=2gl( By conservation of energy from position A to position B )
so we get T_{i}=3mg
3. My Doubt
My doubt was that according to equation 1, the net vertical force is the centripetal force which is radially inwards. So why doesn't the particle go radially upwards to the the centre of the circle's path it is follwing? The same doubt arises for the equations of "FBD of sphere just after touching the nail".. Please reply soon..
Attachments
Last edited: