jforce93
- 26
- 0
Homework Statement
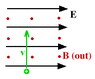
In the figure (see attached) what is the velocity of the charged particle to the nearest tenth of a m/s that will allow it to travel undeflected through the crossed magnetic field if E = 6852 N/C and B = 3.6 T?
Homework Equations
F = E*q + q*V*B
The Attempt at a Solution
Okay, so this is an online physics practice thing (for Giancolli) I was assigned for AP work. It's known for giving wrong (but close) answers, so don't be afraid to tell me that I'm doing this right (or wrong). But the answer I got is very close to the answer it gave me.
Anyway, here is my attempt:
E*q = q*V*B
cross out q
E = V*B
V = E/B
E = 6852 N/C
B = 3.6 T
V = 1903.3 m/s
Thanks,
Jordan