lektor
- 56
- 0
Recently found this question, was hoping someone could help me out or get me started on it >_<
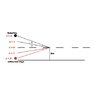
A radio reciever is set up on a mast in the middle of a calm lake to track the radio signal from a satellite orbiting Earth. As the satelllite rises above the horizon, the intensity of the signal varies periodically. The intensity is at a maximum when the satellite is \theta = 3 degrees above the horizon and then again at \theta = 6 degrees above the horizon. What is the wavelength of the satelittle signal? The receiver is h = 4.0 m above the lake surface.
GL
A radio reciever is set up on a mast in the middle of a calm lake to track the radio signal from a satellite orbiting Earth. As the satelllite rises above the horizon, the intensity of the signal varies periodically. The intensity is at a maximum when the satellite is \theta = 3 degrees above the horizon and then again at \theta = 6 degrees above the horizon. What is the wavelength of the satelittle signal? The receiver is h = 4.0 m above the lake surface.
GL