Kile
- 12
- 0
Poster has been reminded that the use of the HH Template and showing work is not optional
Here is diagram for Tower Crane.
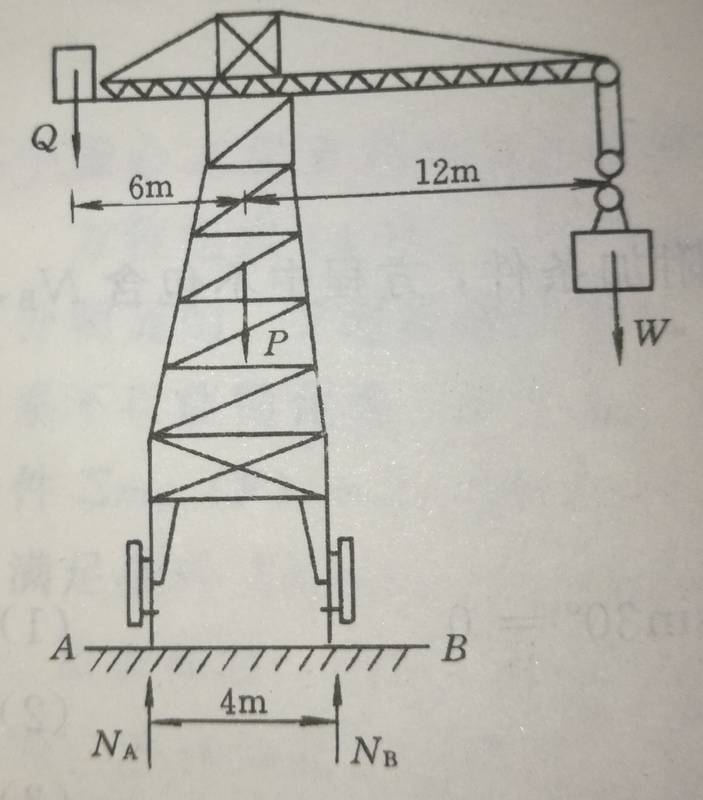
The Rack weight P=700kN, and the maximum load capacity for this crane is W=200kN. The long beam length is 12 metres, and the balance object weighs Q. The short beam length is 6 metres. What is the weight of Q to keep the crane's balance at all situation?
The Rack weight P=700kN, and the maximum load capacity for this crane is W=200kN. The long beam length is 12 metres, and the balance object weighs Q. The short beam length is 6 metres. What is the weight of Q to keep the crane's balance at all situation?