- #1
n77ler
- 89
- 0
[SOLVED] Electric force and charge
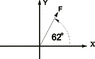
A positive charge of 2.90 μC is at rest at the origin. An electric force of 65.5 x 10-6 N acts on the charge as shown in the figure below. What is the x-component of the electric field at the origin?
F=kQ/r^2
E=kq1q2/r^2
I subbed the charge and force into F=k Q/r^2 and solved for r thinking I could dos somehting with it but it is a hugeeee number so I doubt I am doing it right.
Homework Statement
A positive charge of 2.90 μC is at rest at the origin. An electric force of 65.5 x 10-6 N acts on the charge as shown in the figure below. What is the x-component of the electric field at the origin?
Homework Equations
F=kQ/r^2
E=kq1q2/r^2
The Attempt at a Solution
I subbed the charge and force into F=k Q/r^2 and solved for r thinking I could dos somehting with it but it is a hugeeee number so I doubt I am doing it right.
- in this case, they've told you what the force is, and only asked you to find the field!