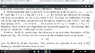
- #1
TheMathNoob
- 189
- 4
Homework Statement
Attached is the problem.
I didn't find anyway to apply the hamming distance to this problem, but I hope that at least this is close to show something.
Homework Equations
The Attempt at a Solution
Lets consider Rn over Z 2 n, so the basis of R n under Z 2 is
(0,0,………0 )all the way until the n coordinate
(1,0,……….0) all the way until the n coordinate
(0,1…………0) all the way until the n coordinate
………………..
(0,0,………….1) all the way until the n coordinateBased on this sequence dim(basis)=n+1
I think that finding the total number of vectors in Rn over Z2 will be useful.
To find the total # of vectors in the vector space spanned by this basis, we can’t use each vector in the basis more than once in each group operation ( I will clarify this later with an example) because for some vectors, it will take us more than 1 unit away from the range. For example (1,0,0…0)+(1,0,0….0)= (2,0,0…) “not allowed”. We won’t take into account the zero vector hence just the vectors with non-zero coordinates will be enough to spanned the other vectors. Taking into account the 0 vector will generate duplicates in the next operation that I am about to performed. We will just use n vectors from the basis hence the 0 vector is discarded. What we are going to trying to do is to find the total number of groups that can be made out of these vectors. In each group, we will perform addition among the vectors and the outcome will be equivalent to one vector in the vector space. The mathematical idea to compute this is doing n choose 0 + n choose 1 + n choose 2+ n choose 3 … +n choose n, this is equal to 2^n-1 without considering the empty set by the binomial theorem. If we add back the 0 vector, the total number of vectors in this vector space is 2^n-1+1=2^n. The n-unit cube in R n over z2 has 2^n vertices, so each vertex must be represented in one coordinate. Hence there are 2^n coordinates, then each vector has to represent one vertex.