What pressure would a strain of 40 µε indicate?

[Al_Pa_Cone]

Q6. A cylindrical vessel 2m internal diameter and 4m long has a wall thickness of 6mm. Strain gauges are installed on the vessel to measure hoop strain (see FIG 6).

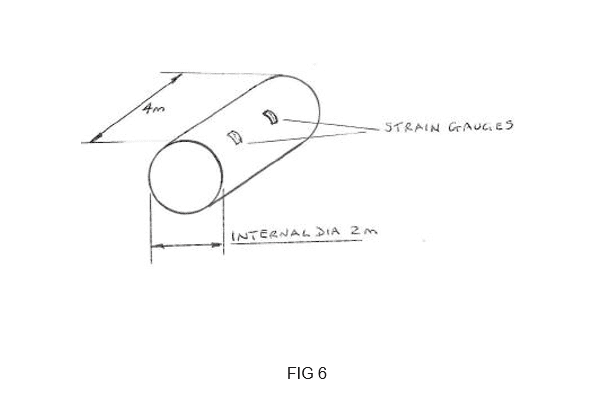
The Young's Modulus of the Material = 290 GN m^-2
The Yield Stress of the Material = 500 MPa

The Questions are
(i) What is the maximum allowable pressure if a factor of safety of 4 is to be used?

(ii) What pressure would a strain of 40με indicate?

For (i) I get:

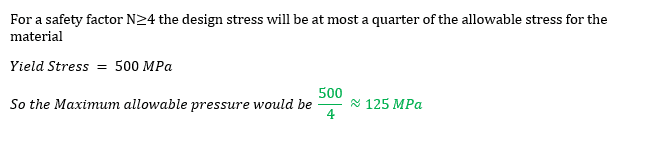
Does this look correct?

for part 2, I cannot find the relevant equation to suit the pressure vessel. I have the hoop equation as
σ = pr/t
Where:
p = Pressure
r = radius of the vessel at 1000mm
t = Thickness of the vessel at 6mm

I am aware the strain is represented as a change in length by 0.000040 but I am not sure how to use this in my working out, given the fact I haven't used the Young's modulus of 290 GN m^-2 either.

Can anyone help me with this question?

 

[mjc123]

(i) No. As your hoop equation indicates, the hoop stress is not equal to the pressure. What pressure would give a hoop stress of 500 MPa?
(ii) What is the definition of Young's modulus? What stress gives a strain of 40 $\mu \epsilon$ ? What pressure causes this stress?

 

[Al_Pa_Cone]

Ok for part (i) This is what I have come up with?

Does this look ok?

I will work on part 2 next.

Thanks

 

[mjc123]

On the right lines, but the radius isn't 2, is it?
So what is the max allowable pressure?

 

[Al_Pa_Cone]

No it isn't you are right, So with a correct radius of 1meter the answer gives 3 MPa. If I follow my original post method that the maximum allowable pressure is 1/4 of this I would get 0.75 MPa or 750000 Pa

 

[Al_Pa_Cone]

To answer part 2 using you advice I have as follows:

 

[Chestermiller]

How does the axial stress affect the hoop strain?

 

[Al_Pa_Cone]

I think the axial stress is twice the hoop stress therefore twice the hoop strain?

 

[Chestermiller]

I think the axial stress is twice the hoop stress therefore twice the hoop strain?

What is the exact equation for the hoop strain as a function of the combination of the hoop stress and the axial stress.

 

[Al_Pa_Cone]

Would this be the relevant equation I am looking for?

 

[Chestermiller]

View attachment 111121

Would this be the relevant equation I am looking for?

No. You need Hooke's law in 3D for conditions of plane stress. Google key words Hooke's Law plane stress.

Are you trying to learn this stuff on your own? Are you using a textbook?

 

[Al_Pa_Cone]

Yes I am a distance learning student at Tees University. I can call a tutor to ask a question over the phone which is not ideal, but basically I try to learn all this in my spare time without assistance.

I covered hookes law several months ago amongst many other things. I have found this forum to be very helpful in providing the assistance I need to arrive at the correct answers.
I will have another look over my previous notes and see what I can dig out. Thanks for your help

 

[Al_Pa_Cone]

I have followed the guidelines in the lessons and obtained this figure for pressure?

If this answer is still wrong I will pursue the Hookes law in 3D method although it is not in the methods provided to me through the University.

Thanks

 

[Al_Pa_Cone]

No it isn't you are right, So with a correct radius of 1meter the answer gives 3 MPa. If I follow my original post method that the maximum allowable pressure is 1/4 of this I would get 0.75 MPa or 750000 Pa

For part one of this Question, Am I right in dividing the answer I obtained (3MPa) by 4 to get the safety factor maximum pressure? or is 3 MPa the answer? I think I need to divide

Thanks

 

[Al_Pa_Cone]

(ii) What pressure would a strain of 40με indicate?

For This part question I have spent some time going back through my lessons provided and found this:

does this look like the correct method to follow in obtaining the pressure value which would cause a strain of 40μ?

This is the last question in my assignment and I am determined to get the highest possible marks. Anyone who can offer help please do.

Thanks

 

[Chestermiller]

For This part question I have spent some time going back through my lessons provided and found this:
View attachment 111304
does this look like the correct method to follow in obtaining the pressure value which would cause a strain of 40μ?

Yes. But, of course, you need to use the corresponding equations involving the stresses and strains in cylindrical coordinates. And don't forget that the stress in the radial direction is much much smaller than the stresses in the axial- and hoop directions, and should thus be taken as zero.

 

[Al_Pa_Cone]

Just to Check, Is part (i) ok now or should I be dividing by 4 for the safety factor? I think I should divide my answer by 4 to get 0.75 MPa maximum allowed pressure?

 

[Chestermiller]

It depends on how they are defining the yield stress.

 

[Al_Pa_Cone]

I can only attempt my answer from the information provided in the initial question. It says the yield stress of the material is 500MPa?

When it mentions the safety factor of 4 I am sure I need to divide the final pressure by 4 to get my result. I just needed a verification I was doing the correct thing?

 

[Chestermiller]

I can only attempt my answer from the information provided in the initial question. It says the yield stress of the material is 500MPa?

When it mentions the safety factor of 4 I am sure I need to divide the final pressure by 4 to get my result. I just needed a verification I was doing the correct thing?

I was asking about the yield criterion that was being used. Some of the choices are Von Mises, Tresca, or maximum tensile stress over all planes of arbitrary orientation. Which criterion do you think they wanted you to use?

 

[Al_Pa_Cone]

I have no idea! I am not that clued up on yield stress sorry.

 

[Chestermiller]

I have no idea! I am not that clued up on yield stress sorry.

See this link https://en.wikipedia.org/wiki/Yield_(engineering)

 

[Al_Pa_Cone]

Thank for providing that link, it was very helpful. According to the information given in the link with regards to Anisotropic yield, This occurs when a metal is subjected to large plastic deformations. As the question states 'What is the maximum allowable pressure if a factor of safety of 4 is to be used?' It doesn't reach the large plastic deformation to use the Anisotropic yield criteria which rules out the use of the von Mises yield criterion. I have copied the details of this link at the bottom of this thread.

So from my lessons on this subject:

So I have the wall Thickness = 6 mm or 0.006 m
The Radius = 1000 mm or 1 m
And the Yeild Stress = 500 MPa

Inuptting these known figures into the above equation and transposing for (P) I have an answer. P = 3 MPa.

In the lesson notes It mentions ' In the absence of a code, we will use N > 4 (i.e the design stress will be at most a quater of the allowable stress for the material.)'
Well the yeild stress is 500 MPa and the pressure I have worked out to be 3 MPa. So if a 3 MPa pressure would cause a yeild of 500 MPa then a safety factor of 4 would require me to divide this firgure by 4 giving Pressure = 0.75 to create a yeild of 125 MPa?

Does this look like it could be a correct answer or am I missing something? from my previous questions, my history would suggest I am missing something.

Anisotropic yield criteria
When a metal is subjected to large plastic deformations the grain sizes and orientations change in the direction of deformation. As a result, the plastic yield behavior of the material shows directional dependency. Under such circumstances, the isotropic yield criteria such as the von Mises yield criterion are unable to predict the yield behavior accurately. Several anisotropic yield criteria have been developed to deal with such situations. Some of the more popular anisotropic yield criteria are:

• Hill's quadratic yield criterion
• Generalized Hill yield criterion
• Hosford yield criterion

 

[Al_Pa_Cone]

Also, This is what I have obtained as a final answer to part b?
with the 3dimentional method I would need the poissons ratio and also I came up against a complication in measuring the x and y stresses when they would be acting on the rounded edges of the cylinder? what surface area would I use in the equation provided stress = force/ cross sectional area?

I have gone with what I think is the correct method. Can anyone verify this?

 

[Chestermiller]

Thank for providing that link, it was very helpful. According to the information given in the link with regards to Anisotropic yield, This occurs when a metal is subjected to large plastic deformations. As the question states 'What is the maximum allowable pressure if a factor of safety of 4 is to be used?' It doesn't reach the large plastic deformation to use the Anisotropic yield criteria which rules out the use of the von Mises yield criterion. I have copied the details of this link at the bottom of this thread.

You are not interpreting it correctly. The von Mises yield criterion is fine for determining the onset of yield even for small deformations.

So from my lessons on this subject:
View attachment 111333

OK. So they are indicating that you should use the maximum principal stress criterion to establish the yield point.

So I have the wall Thickness = 6 mm or 0.006 m
The Radius = 1000 mm or 1 m
And the Yeild Stress = 500 MPa

Inuptting these known figures into the above equation and transposing for (P) I have an answer. P = 3 MPa.

In the lesson notes It mentions ' In the absence of a code, we will use N > 4 (i.e the design stress will be at most a quater of the allowable stress for the material.)'
Well the yeild stress is 500 MPa and the pressure I have worked out to be 3 MPa. So if a 3 MPa pressure would cause a yeild of 500 MPa then a safety factor of 4 would require me to divide this firgure by 4 giving Pressure = 0.75

Correct

to create a yeild of 125 MPa?

No. The yield stress is a property of the material, and is independent of the loading. At 125 MPa, the material will not yield.

 

[Chestermiller]

Also, This is what I have obtained as a final answer to part b?
with the 3dimentional method I would need the poissons ratio and also I came up against a complication in measuring the x and y stresses when they would be acting on the rounded edges of the cylinder? what surface area would I use in the equation provided stress = force/ cross sectional area?

I have gone with what I think is the correct method. Can anyone verify this?

View attachment 111334

No. This is not done correctly. The strain in the hoop direction is given by: $$\epsilon_{\theta}=\frac{\sigma_{\theta}-\nu \sigma_z}{E}$$where $$\sigma_{\theta}=\frac{pr}{t}$$ and $$\sigma_z=\frac{pr}{2t}$$

 

[Al_Pa_Cone]

With this method, I am left with 3 unknown values in the first equation and 2 unknown values in the sub equations.

If don't have the value for Stress in each of the two how can I get a value for pressure? and also the poissons ratio is still unknown in the first equation?

This Is my last assignment question and I was really hoping I had completed it as I have spent weeks on this one! I don't know where to start with this one then.

 

[Chestermiller]

With this method, I am left with 3 unknown values in the first equation and 2 unknown values in the sub equations.View attachment 111346
If don't have the value for Stress in each of the two how can I get a value for pressure? and also the poissons ratio is still unknown in the first equation?

This Is my last assignment question and I was really hoping I had completed it as I have spent weeks on this one! I don't know where to start with this one then.

You solve the strain equation, treating the pressure P as an unknown. This can't be done properly without knowing the Poisson ratio. Assume a typical value of 0.3.

 

[Al_Pa_Cone]

Wow! how am I supposed to transpose that for P? I am not to bad at transposition but that looks a nightmare!

 

[Chestermiller]

View attachment 111350
Wow! how am I supposed to transpose that for P? I am not to bad at transposition but that looks a nightmare!

In first year (9th grade) algebra, we learned how to solve a linear algebraic equation in one unknown. Apply what you learned there.

 

[Al_Pa_Cone]

Thanks for that put down! everyone doesn't come from the same level of education. I haven't used the minimal algebra I was taught in school for over 15 years until I started this course. I came on this forum for guidance not answers. I am fully prepared to attempt all of the questions I post first, I was merely expressing my concern at a transposition problem out loud.

Once I get time tomorrow, I will work my way through and post my results.

 

[Chestermiller]

Thanks for that put down! everyone doesn't come from the same level of education. I haven't used the minimal algebra I was taught in school for over 15 years until I started this course. I came on this forum for guidance not answers. I am fully prepared to attempt all of the questions I post first, I was merely expressing my concern at a transposition problem out loud.

Once I get time tomorrow, I will work my way through and post my results.

I am truly very sorry. No excuse. I won't let that happen again. Here's what you get when you factor the right hand side of the equation (and correct a few arithmetic errors and typos):

$$0.00004=\left[\frac{\frac{1}{0.006}-0.3\frac{1}{(2)(0.006)}}{210000\ MPa}\right]P$$
Is the Young's modulus 210 GPa or 290 GPa (as in post #1)?

 

[Al_Pa_Cone]

I haven't taken any offence by your previous comments but thanks for accepting, it wasnt a helpful reply.

I had noticed the 0.0006 typo when it should have been 0.006 but I missed the 210! good spot. I find transposition very interesting and I like to try and solve these problems myself by substituting unknown values with simple numbers to see what works and what is acceptable. The factorising part was a little more advanced to the basic transposition as I couldn't figure out how to get both values of P into 1 P. I will look back over my maths bridging course and try to refresh my memory on how to achieve it.

Thanks for the help!

 

[Al_Pa_Cone]

Does This look ok?

 

[Al_Pa_Cone]

Sorry there was a problem with my answer when I didnt use a bracket when typing in 2*0.006 so it seperated.

This is my answer?

 

[Chestermiller]

View attachment 111406
Sorry there was a problem with my answer when I didnt use a bracket when typing in 2*0.006 so it seperated.

This is my answer?

Yes. Of course, you'll need to do the arithmetic on the right hand side to come up with an actual number.

 

[Al_Pa_Cone]

Yes, I just wanted to check my method of transposition was correct prior to any further calculations. I have worked out the answer to be 81.88 x 10^-3 MPa

Does this look good?

 

[Chestermiller]

Yes, I just wanted to check my method of transposition was correct prior to any further calculations. I have worked out the answer to be 81.88 x 10^-3 MPa

Does this look good?

Yes, aside from a need to address the significant figures issue. Your answer is the same as 82 KPa.

 

[Al_Pa_Cone]

Great! Thank you!

 

[electr]

hello,i am stuck with the last question,how you get the 81.88 Mpa?i tryed the equation you used but it gives different number,didyou used a different equation for the solution?i d appreciate your help,thx in advance

 

[Al_Pa_Cone]

what have you got so far?

 

[electr]

P = (290000/ 1/0.006 - 0.3 x 1/2 x 0.006) x 0.00004 = 0.0008367398 ,i used the equation that chestermiller suggested you to use,is this wrong?completelly stuck on this problem,didnt plan to combine the two equations,and we miss the poisons ratio that's why i saw your solution but didnt what you got,got any idea?

 

[Al_Pa_Cone]

I will take a look back through this tonight when i get a chance. I think you may have a rounding error somewhere.
I had to factorise the equation and transpose it to get my answer, but it was a jerk to figure out.

Are you doing your HNC at tees uni as well then?

 

[electr]

thank for your help i m not here to get just the answers because i want to learn these things but i got stuck with this one,i coudnt find a solution, i saw your posts and it was the only way to find a answer but i coudnt get the numbers...,yes i m doing the HNC at tees,very convenient because i work and i can study when i can,,for the first question you divided by 4 to get the right number or the 3 Mpa is enough? I will wait for your reply,thank you again

 

[Al_Pa_Cone]

I think your problem is the brackets are missing around the denominator part of that equation. It should be:

Also I received some good advice from a guy on here, it was reflected in my mark from the tutor when he commented on my assignment. The advice was to write down the units into the equations as well, because it helps find out where mistakes have been made.

[(290000 G Nm^-2 ) / (1 m / 0.006 m) - 0.3 x (1 m / (2 x 0.006 m)) ]x 0.00004 = P

This input into a scientific calculator would give the answer 81.88 x 10^-3 in Mega Newtons which is equal to 82 kN when rounded

 

[Al_Pa_Cone]

how many modules have you done then? maybe you could help me with some of my other assignments?

 

[martinsyde]

Hi Al, how did you go with question 5 part c of this assignment? I'm also doing the same tees assignments as you but hit a wall on q5c. I've slipped up by having to work a lot lately and am struggling to get back into it!

 

[Al_Pa_Cone]

...

 

[martinsyde]

I have made several attempts but keep going wrong, I've followed you last thread on it but can see how you made it work? i can't get the EI side of it out of my head as I've worked that out to be 113.4knm and that don't fit into you way of working. I'm going to work for a couple of hours now and going to have a go when i get back in, if it can't get it I'm going to do question 6 and submit it see if i get a pass!
Out of interest this is my 4th module, how far on are you?

 

[Al_Pa_Cone]

...