What's wrong with my math?[Thermal volume expansion]

[Kuzon]

Homework Statement

Homework Equations

Coefficient of water expansion for volume given by the textbook is 207 x 10^-6

The Attempt at a Solution

[/B]
I did 80.4*0.000207*0.000369 = 0.00000614119 m^3

 

[SteamKing]

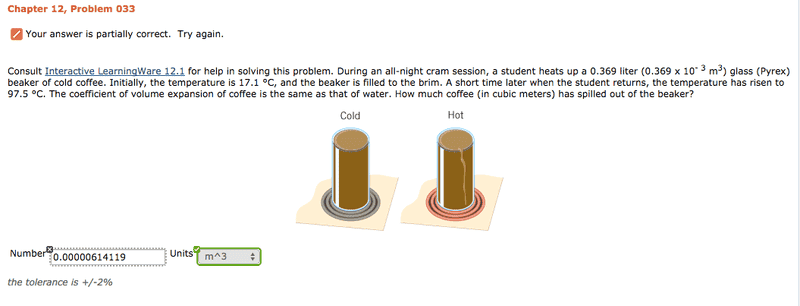
Homework Statement

Homework Equations

Coefficient of water expansion for volume given by the textbook is 207 x 10^-6

The Attempt at a Solution

[/B]
I did 80.4*0.000207*0.000369 = 0.00000614119 m^3

Your response was flagged probably because you didn't use the right number of significant figures in your answer.

 

[Kuzon]

Your response was flagged probably because you didn't use the right number of significant figures in your answer.

No the website does not care about rounding, there is just a +/- 2% tolerance on the right answer. Can you see anything wrong with the math?

 

[SteamKing]

No the website does not care about rounding, there is just a +/- 2% tolerance on the right answer. Can you see anything wrong with the math?

Rounding and significant figures are not the same. Your math appears to be correct; your answer is too precise given the precision of the data.

 

[Kuzon]

Rounding and significant figures are not the same. Your math appears to be correct; your answer is too precise given the precision of the data.

Yes but that doesn't matter is what I mean. All they mark on is that it's within the +/- 2% tolerance range of the correct answer. You could have a million 5s after your correct answer for all they care. Thanks for checking my math though, I don't know what's wrong - maybe the wrong coefficient of volume expansion for water? Apparently it changes depending on what temperature water is at?

 

[ehild]

The Pyrex beaker expands, too. You can find its thermal expansion coefficient here: https://en.wikipedia.org/wiki/Borosilicate_glass. It does not change the result much, but your solution in, principle, is not correct, . The expansion coefficient of water also changes with the temperature, but I do not think you are supposed to take it into account. Otherwise it should have been given.

 

[haruspex]

According to http://www.engineeringtoolbox.com/water-thermal-properties-d_162.html, the thermal expansion coefficient you quote is correct at 20C. It goes up substantially with increasing temperature. Using the chart at that link, I calculate an expansion of 4% for the whole temperature increase (as opposed to 1.6%).

 

[Kuzon]

The Pyrex beaker expands, too. You can find its thermal expansion coefficient here: https://en.wikipedia.org/wiki/Borosilicate_glass. It does not change the result much, but your solution in, principle, is not correct, . The expansion coefficient of water also changes with the temperature, but I do not think you are supposed to take it into account. Otherwise it should have been given.

I have no idea how to work out the answer if the pyrex beaker expands also though :/

 

[SteamKing]

You might need to incorporate the expansion of the Pyrex beaker due to the increase in temperature.

IDK if your text has a value for the expansion of Pyrex glass, but the linear coefficient α = 3.2 × 10^-6 K^-1 @ 20° C

https://en.wikipedia.org/wiki/Thermal_expansion

I have no idea how to work out the answer if the pyrex beaker expands also though :/

Why not? When the Pyrex beaker expands, its volume increases slightly, but not as much as that of the coffee inside. The volume increase of the coffee doesn't depend on how much the beaker expands, but the amount of coffee spilled will be affected.

 

[Kuzon]

You might need to incorporate the expansion of the Pyrex beaker due to the increase in temperature.

IDK if your text has a value for the expansion of Pyrex glass, but the linear coefficient α = 3.2 × 10^-6 K^-1 @ 20° C

https://en.wikipedia.org/wiki/Thermal_expansion

Why not? When the Pyrex beaker expands, its volume increases slightly, but not as much as that of the coffee inside. The volume increase of the coffee doesn't depend on how much the beaker expands, but the amount of coffee spilled will be affected.

So I see the values it gives for pyrex are 3.3*10^-6 for linear and 9.9*10^-6 for volume. But how do I calculate how much the volume of the pyrex jug changes because it's hollow? I'm not sure how I would calculate it :/ could you please help me?

 

[haruspex]

So I see the values it gives for pyrex are 3.3*10^-6 for linear and 9.9*10^-6 for volume. But how do I calculate how much the volume of the pyrex jug changes because it's hollow? I'm not sure how I would calculate it :/ could you please help me?

Assuming the Pyrex expands linearly in all directions, what do you think the increase in volume of the cavity would be?
But as @ehild says, it will make very little difference to the answer. Did you read my post #7?

 

[Kuzon]

Assuming the Pyrex expands linearly in all directions, what do you think the increase in volume of the cavity would be?
But as @ehild says, it will make very little difference to the answer. Did you read my post #7?

Yeah, I'm pretty sure that the coefficient I used is correct though, the pyrex thingy seems to be all I need to add to my math to fix it. But I still have no idea what the answer will be if the jug expands linearly... Can you help me on the calculations?

 

[haruspex]

Yeah, I'm pretty sure that the coefficient I used is correct though, the pyrex thingy seems to be all I need to add to my math to fix it. But I still have no idea what the answer will be if the jug expands linearly... Can you help me on the calculations?

Imagine a solid cylinder of Pyrex with the same outside dimensions as the beaker. You know what that would expand to. Now think of that solid cylinder as the beaker filled with a solid cylinder of Pyrex. That would expand exactly the same right? And you would not expect a gap to open up between cylinder and beaker (or the solid cylinder would have split under internal stresses). So...

The end difference to your answer should be about 5%.

 

[Kuzon]

Imagine a solid cylinder of Pyrex with the same outside dimensions as the beaker. You know what that would expand to. Now think of that solid cylinder as the beaker filled with a solid cylinder of Pyrex. That would expand exactly the same right? And you would not expect a gap to open up between cylinder and beaker (or the solid cylinder would have split under internal stresses). So...

The end difference to your answer should be about 5%.

I still don't understand sorry, is there any chance you could you tell me how to solve it?

 

[haruspex]

I still don't understand sorry, is there any chance you could you tell me how to solve it?

To make it a little simpler, consider two solid spheres of radii r and r+dr. If heated to the same extent, you'd expect their volumes to increase in the same ratio, right? Now think of the larger sphere as consisting of a sphere of radius r surrounded by a shell of thickness dr. By what ratio has the space inside the shell increased? Is it different from the ratios by which the solid spheres increased?

 

[Kuzon]

Imagine a solid cylinder of Pyrex with the same outside dimensions as the beaker. You know what that would expand to. Now think of that solid cylinder as the beaker filled with a solid cylinder of Pyrex. That would expand exactly the same right? And you would not expect a gap to open up between cylinder and beaker (or the solid cylinder would have split under internal stresses). So...

The end difference to your answer should be about 5%.

I got it thanks! You just treat the pyrex jug as if it's solid and solve for the change in volume! It doesn't change if it's hollow.

 

[haruspex]

I got it thanks! You just treat the pyrex jug as if it's solid and solve for the change in volume! It doesn't change if it's hollow.

Right.