Solving Wheatstone Bridge w/ R1=2000, R2=3000, R3=4000 & 12V Battery

[control]

Homework Statement

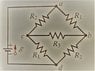
Set voltage between 1. a-b; 2- b-c; 3 c-d 4. a-c; if voltage of battery is 12V and R_1=2000 ohms R_2=3000 ohms; R_3= 4000 ohms. (see attached file)

Homework Equations

voltage=final voltage- innitial voltage
resistors in series R_1,2=R_1+R_2
parallel resistors: R_1,2=(R_1*R_2)/(R_1+R_2)

The Attempt at a Solution

I have no idea how to solve such problem. I can use Kirchhoff laws in circuits, I can use all equations I wrote in "relevant equations", I watched video how to set equivalent resistance of those resistors through "delta to ypsilon transformation" () but I have absolutely no idea how to apply my knowledge in such problem.

 

[gneill]

I can use Kirchhoff laws in circuits, I can use all equations I wrote in "relevant equations"

Good. So that means you can write the KVL loop equations for the circuit (or the KCL node equations). What do you get?

 

[control]

Well, resistance of equivalent resistor would be R_eq=2461.44 ohms.
KVL loop looks: +voltage of battery-(current*equivalent resistor)=0 => 12volts-current*2461.44ohms=0 => current=0.004875ampers
So what should I do next?

 

[gneill]

Well, resistance of equivalent resistor would be R_eq=2461.44 ohms.
KVL loop looks: +voltage of battery-(current*equivalent resistor)=0 => 12volts-current*2461.44ohms=0 => current=0.004875ampers
So what should I do next?

You have not solved the circuit. You need to either solve for loop currents (using KVL loop equations) or for node voltages (KCL node equations). My own preference would be to write node equations for the two essential nodes (b and c) since the problem is asking for potential difference between nodes.

 

[control]

You mean:
-I_3*R_1-I_2*R_3+I_1*R_2=0
-I_2*R_3-I_4*R_1+I_5*R_2=0
I_1+I_2=I_4
I_3=I_2+I_5
?

 

[gneill]

That's a start. You need one more loop, one involving the voltage source.

 

[control]

There should be two loops involving source:
ε-R_1*I_3-R_2*I_5=0
ε-R_2*I_1-R_1*I_4=0

 

[gneill]

There should be two loops involving source:
ε-R_1*I_3-R_2*I_5=0
ε-R_2*I_1-R_1*I_4=0

Okay, but you'll only need one of them; you need just enough loops so that every component is included in at least one of the loops. After that any additional loops will not introduce any new (independent) information to the system of equations.

 

[control]

Ok, so now I choose 5 equations with 5 unknown currents, find them and using Ohm´s law I will find voltage on resistors?

 

[gneill]

Ok, so now I choose 5 equations with 5 unknown currents, find them and using Ohm´s law I will find voltage on resistors?

Yes. Three loop equations and two node equations (KCL at two of the nodes).

If I may make a suggestion, you can reduce the number of current unknowns if you are careful about how you introduce new currents when you label your circuit. Proceed systematically and only introduce the minimum number of new currents required at junctions. For example, if one current (say $i_1$) enters a junction and two leave, then only introduce one new current (say $i_2$) leaving the junction by one of the paths so that $i_1 - i_2$ leaves by the other. If you do it this way you're effectively doing the KCL sums ahead of time and you'll end up with the minimum number of current variables required and you'll only require loop currents to solve.

 

[control]

OK, thanks a lot.