Meadow_Lark
- 8
- 0
I am so confused by this question. I do not have a clue what I am supposed to do here. Can you please help??
[1pt] For each ith revolution, at what time point does the disc reach its average angular velocity? For example, for the 10th revolution what is the total elapsed time from the beginning of the first revolution to the point in the 10th revolution when the angular velocity of the disc is equal to the average angular velocity you plotted in Q6 for revolution number 10?
Assume that time t=0 at the beginning of the first revolution (i = 1).
Give a formula for this and use your answer in Q8 to guide you. It may help to do this first for the cases (i = 1) and (i = 2), then generalize.
Below are the 2 questions and corresponding answers referenced above.
Q6: Provide a graph of the average angular velocity vs. revolution number for three data sets your group recorded. All data sets should appear on a single graph.
Graph from Q6:
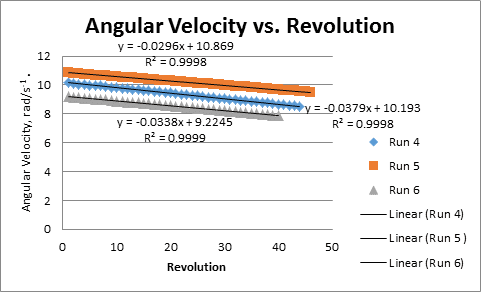
Q 8: In order to find the angular acceleration, we need to make a graph that has angular velocity on the vertical axis and time on the horizontal axis. What we determined before for Q6 was average angular velocity and revolution number. We now need to assign a time value to each average angular velocity point we computed so we can build a new graph of angular velocity vs. time.
Let’s assume that the spinning disc accelerates (or decelerates as the case may be) at a constant rate. For any given revolution, the average acceleration value you plotted for it in Q6 should be reached at:
Answer from Q8:
D) ½ of the way through the revolution
[1pt] For each ith revolution, at what time point does the disc reach its average angular velocity? For example, for the 10th revolution what is the total elapsed time from the beginning of the first revolution to the point in the 10th revolution when the angular velocity of the disc is equal to the average angular velocity you plotted in Q6 for revolution number 10?
Assume that time t=0 at the beginning of the first revolution (i = 1).
Give a formula for this and use your answer in Q8 to guide you. It may help to do this first for the cases (i = 1) and (i = 2), then generalize.
Below are the 2 questions and corresponding answers referenced above.
Q6: Provide a graph of the average angular velocity vs. revolution number for three data sets your group recorded. All data sets should appear on a single graph.
Graph from Q6:
Q 8: In order to find the angular acceleration, we need to make a graph that has angular velocity on the vertical axis and time on the horizontal axis. What we determined before for Q6 was average angular velocity and revolution number. We now need to assign a time value to each average angular velocity point we computed so we can build a new graph of angular velocity vs. time.
Let’s assume that the spinning disc accelerates (or decelerates as the case may be) at a constant rate. For any given revolution, the average acceleration value you plotted for it in Q6 should be reached at:
Answer from Q8:
D) ½ of the way through the revolution