I When does the exchange operator commute with the Hamiltonian

[aliens123]

I am attaching an image from David J. Griffith's "Introduction to Quantum Mechanics; Second Edition" page 205.

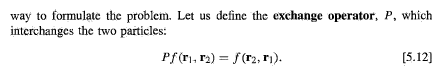
In the scenario described (the Hamiltonian treats the two particles identically) it follows that
$$PH = H, HP = H$$
and so $$HP=PH.$$

My question is: what are the necessary and sufficient conditions to have that $$[P,H]=0?$$ Clearly
$$PH = H, HP = H$$
is sufficient, but is it necessary?

Also, as a bonus question, because the exchange operator is an observable, what would it mean to "measure" this in a laboratory?

 

[PeterDonis]

In the scenario described (the Hamiltonian treats the two particles identically)

That's not the key point: the key point is that the two particles are identical. In other words, if we have a quantum system consisting of two electrons, for example, they are identical particles, so the Hamiltonian must treat them the same, so the exchange operator must commute with the Hamiltonian.

But if we have a quantum system consisting of an electron and a proton, for example, they are not identical particles so the Hamiltonian will not necessarily treat them the same, so the operator that exchanges them might not commute with the Hamiltonian.

 

[aliens123]

so the Hamiltonian must treat them the same, so the exchange operator must commute with the Hamiltonian.

Why is it the case that if the Hamiltonian treats them the same, then the exchange operator must commute with the Hamiltonian? Can you prove this?

 

[PeroK]

Why is it the case that if the Hamiltonian treats them the same, then the exchange operator must commute with the Hamiltonian? Can you prove this?

Can you tell us what you think the Hamiltonian represents?

 

[aliens123]

Can you tell us what you think the Hamiltonian represents?

Energy

 

[PeroK]

Energy

I would have said that it is the operator that represents the total energy of the system.

I was then going to ask how the total energy is affected when you exchange two identical particles?

 

[aliens123]

I would have said that it is the operator that represents the total energy of the system.

I was then going to ask how the total energy is affected when you exchange two identical particles?

Intuitively speaking I have no trouble with the concept that the energy shouldn't be "affected" by exchanging two identical particles. I guess what I am looking for is a more formal way of demonstrating that the operators must commute; i.e. how could you prove this to a stubborn person with no physical intuition whatsoever based solely on the definitions of the operators.

Furthermore, two operators which are Hermitian and therefore observables commute if and only if we can simultaneously measure one observable then measure the other without "affecting our knowledge" of the previously measured quantity. But what would it mean to make a measure of the exchange operator?

 

[PeroK]

Intuitively speaking I have no trouble with the concept that the energy shouldn't be "affected" by exchanging two identical particles. I guess what I am looking for is a more formal way of demonstrating that the operators must commute; i.e. how could you prove this to a stubborn person with no physical intuition whatsoever based solely on the definitions of the operators.

Furthermore, two operators which are Hermitian and therefore observables commute if and only if we can simultaneously measure one observable then measure the other without "affecting our knowledge" of the previously measured quantity. But what would it mean to make a measure of the exchange operator?

An observable is represented by a Hermitian operator, but it's a moot point whether every Hermitian operator represents an observable. The identity operator is Hermitian, for example. In any case, whether the exchange operator represents an observable doesn't affect its properties.

If you have a system involving two identical particles, then it would be an elementary test of a proposed Hamiltonian that it commuted with the exchange operator. If you produced an operator that did not commute with the exchange operator, then that would disqualify it from being the valid Hamiltonian for the system.

That's how I would justify things.

 

[aliens123]

If you produced an operator that did not commute with the exchange operator, then that would disqualify it from being the valid Hamiltonian for the system.

What about something like the following:

Suppose that $$\Psi(r_1, r_2)$$ are eigenstates of the Hamiltonian(s) $$H(r_1, r_2).$$
Then
$$H(r_1, r_2)\Psi(r_1, r_2) = E \Psi(r_1, r_2) $$
for some scalar $$E.$$
Furthermore, because the labeling is arbitrary at this point,
$$H(r_2, r_1)\Psi(r_2, r_1) = E \Psi(r_2, r_1) $$
for the same scalar $$E.$$

Now suppose that $$H(r_1, r_2) = H(r_2, r_1).$$
Then
$$ H(r_1, r_2)\Psi(r_1, r_2) = E \Psi(r_1, r_2)$$
and
$$ H(r_2 r_1)\Psi(r_2, r_1) = H(r_1 r_2)\Psi(r_2, r_1) = E \Psi(r_2, r_1)$$
Then, because $$\Psi(r_1, r_2)$$ and $$\Psi(r_2, r_1)$$ have the same eigenvalue under the same Hermitian operator $$H(r_1 r_2)$$ it follows that they are the same vector (we assume they are normalized) up to a phase.

Now
$$PH\Psi = P(E \Psi) = EP\Psi = E\phi \Psi$$
$$HP\Psi = H(\phi \Psi) = \phi H\Psi = \phi E\Psi$$
So
$$[P,H]=0.$$

 

[PeterDonis]

Why is it the case that if the Hamiltonian treats them the same, then the exchange operator must commute with the Hamiltonian?

You already answered this in your OP:

In the scenario described (the Hamiltonian treats the two particles identically) it follows that
$$
PH = H, HP = H
$$
and so
$$
HP = PH
$$

 

[aliens123]

You already answered this in your OP:

I think that what I wrote in the OP was wrong, shouldn't it instead be:
$$PH = \pm H, HP = \pm H$$

Regardless, my question in the OP was "the above is sufficient, but is it necessary?"

I am trying to find an argument which doesn't make reference to physical intuition, and instead relies only on the definitions of the operators. Of course, a system with two identical particles is a physical requirement, but how can we state this as some mathematical condition, and then use that mathematical condition to show what we desire?

 

[PeterDonis]

I think that what I wrote in the OP was wrong, shouldn't it instead be:
$$
PH = \pm H, HP = \pm H
$$

Strictly speaking, yes. But $PH = HP$ is still valid.

Of course, a system with two identical particles is a physical requirement, but how can we state this as some mathematical condition

Griffiths states it, but not very explicitly. He is assuming the standard non-relativistic Hamiltonian for two particles:

$$
H = \frac{p_1^2}{2m_1} + \frac{p_2^2}{2m_2} + V(r_1, r_2)
$$

Then "identical particles" means, as he says, that $m_1 = m_2$ and $V(r_1, r_2) = V(r_2, r_1)$, i.e., the potential is symmetric between the two particles. Then the Hamiltonian becomes

$$
H = \frac{p_1^2 + p_2^2}{2m} + V(r_1, r_2)
$$

It should be easy to see from the above that for any $\psi$, $H P \psi = P H \psi$. Or, to put it another way, it doesn't matter whether you switch the $1$ and $2$ subscripts on the $p$'s and $r$'s before or after you evaluate $H$.

 

[aliens123]

Strictly speaking, yes. But $PH = HP$ is still valid.
Griffiths states it, but not very explicitly. He is assuming the standard non-relativistic Hamiltonian for two particles:

$$
H = \frac{p_1^2}{2m_1} + \frac{p_2^2}{2m_2} + V(r_1, r_2)
$$

Then "identical particles" means, as he says, that $m_1 = m_2$ and $V(r_1, r_2) = V(r_2, r_1)$, i.e., the potential is symmetric between the two particles. Then the Hamiltonian becomes

$$
H = \frac{p_1^2 + p_2^2}{2m} + V(r_1, r_2)
$$

It should be easy to see from the above that for any $\psi$, $H P \psi = P H \psi$. Or, to put it another way, it doesn't matter whether you switch the $1$ and $2$ subscripts on the $p$'s and $r$'s before or after you evaluate $H$.

Hi, thank you for your replies.

I can "see" intuitively in some sense that for any $\psi$, $H P \psi = P H \psi$, but how would you prove this? I already made an attempt in a previous post (which you may or may have not seen), but I am not sure if my argument is correct, or if there is a simpler, easier way. It seems like it should maybe be very easy and obvious.

 

[PeterDonis]

how would you prove this?

By "easy to see" I meant "easy to prove". Try explicitly computing $H (P \psi)$ and $P (H \psi)$, using the $H$ I previously posted. Doing it for an eigenstate of $H$, as you did in your earlier post, is sufficient for a proof for all states (can you see why?), and makes the computation easier. (Also note that I wrote $p$ for momentum in my previous post, but $p$ is an operator so you need to use its position representation, which is $p = - i \hbar \nabla$, so $p^2 = \hbar^2 \nabla^2$.)