- #1
Low-Q
Gold Member
- 284
- 9
This is an experiment with gyros on a wheel.
First of all, this is not a homework question - I am just a 40 year old man with general interests in physics.
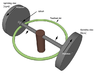
Example: I have a wheel. Attached to its circumference, there are placed heavy discs that is aligned tangentially. These discs are connected to a gear mechanism which will let the discs start spinning fast when the wheel is turned around slowly.
All these discs are now gyros which will resist any change in alignment as they are spinning fast tangentially at the circumference of the wheel.
Initially I must add energy to accelerate the wheel. Now, to maintain a given RPM of the wheel, I must constantly add energy to it, even if friction is not present, because the gyros will try to stop the wheel from turning around.
Where do the input energy go? I ask because in this experiment, I cannot (appearently) get back the energy I add to the wheel except for portions of the energy I added during acceleration. I appearently waste energy that for some reason just disappear. There is no fricton, so there is not generating heat, or other forms of radiation.
Can somebody please explain why it appearently is no conservation of energy in this experiment?
I can make a brief drawing of the experiment if that helps.
Br.
Vidar
First of all, this is not a homework question - I am just a 40 year old man with general interests in physics.
Example: I have a wheel. Attached to its circumference, there are placed heavy discs that is aligned tangentially. These discs are connected to a gear mechanism which will let the discs start spinning fast when the wheel is turned around slowly.
All these discs are now gyros which will resist any change in alignment as they are spinning fast tangentially at the circumference of the wheel.
Initially I must add energy to accelerate the wheel. Now, to maintain a given RPM of the wheel, I must constantly add energy to it, even if friction is not present, because the gyros will try to stop the wheel from turning around.
Where do the input energy go? I ask because in this experiment, I cannot (appearently) get back the energy I add to the wheel except for portions of the energy I added during acceleration. I appearently waste energy that for some reason just disappear. There is no fricton, so there is not generating heat, or other forms of radiation.
Can somebody please explain why it appearently is no conservation of energy in this experiment?
I can make a brief drawing of the experiment if that helps.
Br.
Vidar