CKH
- 194
- 7
Some thoughts about the twin paradox (with a new question/paradox at the end):
Beginners, like myself, when confronting the twin paradox often want to know where it is that the traveling twin loses so much time. A frustrated poster trying to explain the paradox posted this:
Still, the beginner is persistent in wanting to know where these clocks differ along the trip and by how much. There is no single answer due to the relativity of simultaneity but there are some approaches.
To answer this question, one approach is to explain what each twin sees (e.g. with a powerful telescope) on the other's clock. In this case a Doppler effect occurs in the clocks readings due to relative motion. Thus this description of the relationship between the clocks has a complicating factor: the delays in the readings by each twin of the other's clock are changing due to the the changing distance between the twins.
But there is another way of viewing the relationship between the clocks.
In the simple twin paradox, one twin stays at home and the other travels to a distant destination and back again at a substantial fraction of the speed of light. We can assume that the traveling twin accelerates to a fixed speed almost instantaneously when he leaves, when he turns around and that he stops quickly when he returns home. The traveling twin moves with constant velocity on the long outbound and inbound legs of the journey.
With this scenario in mind, here's another clock comparison method:
Prior to the trip, a number of clocks are placed at intervals along the path that the traveler will take to the destination.
All of these clocks along the path to the destination are placed so that they are stationary wrt the home clock. That is, all these clocks are at rest in the same inertial frame with the home clock.
Using Einstein's clock synchronization method, we synchronize all of these clocks with the home clock.
The clocks along the traveler's path then represent "home clock time" in the home clock's inertial frame. Since this frame is inertial throughout the trip we know that the established synchronization of these clocks with the home clock persists throughout, in the home frame.
The traveler can read these distributed "home clocks" during his trip and compare them with the readings with his own clock. Then he has an answer to how and where he is losing time relative to the home clock. The comparison is illustrated in this diagram linked from http://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters_2013_Jan_1/spacetime_tachyon/index.html (sorry for the size):
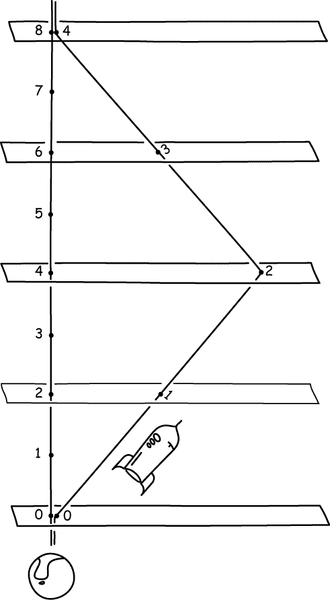
Copyright John D. Norton. January 2001, September 2002; July 2006; February 3, 2007; January 23, September 24, 2008; January 21, 2010; February 1, 2012.
In the diagram the rocket twin travels at 86.6% the speed of light resulting in a time dilation factor of 1/2. The straight vertical path is the home clock's path over time (the home clock's worldline). The dogleg is the traveler's worldline. Each is marked with the proper time in years on each of the twin's clocks. The horizontal planes show the positions of the home clocks (imagine the line of clocks) and of the traveler at different times in the home frame.
The travel reads the "home time" using the clocks placed along the plane. The traveler finds the following correspondence between home time and the time on the own clock (as shown in the diagram):
Clock readings in years
Home Traveler
0 0
2 1
4 2
6 3
8 4
When the traveler returns he can show the home twin the above record, so the home twin can know in his own frame how old the traveler was when he was a certain age.
There is no mystery about where these clocks get out of sync from this perspective. They do it uniformly along the entire trip.
Acceleration does not directly affect the clocks, it is the speed of the traveler and the time over which he travels with that speed that determines the age gap. The above clock comparison exactly reflects the time dilation of the traveling twin which is constant throughout the trip.
Note that the traveling twin could, instead of traveling far away, make small circles around home at the same speed for the same amount of time and the clock results would be the same. So it appears that it has little to do with how far away he travels.
Acceleration does not affect the age difference directly but the acceleration is necessary to follow any non-straight path through flat spacetime.
The twin paradox is "why can't we just reverse the role of the home and traveler in the diagram, such that the traveler is considered stationary and the home clock is considered to move, so that the traveler gets older instead"? We cannot because the traveler's path through spacetime cannot be made a straight line in any such diagram. It is a dogleg in all inertial frames, while the path of the home clock is straight in all inertial frames.
Caveats:
1) There is no unique way to compare the clock readings, some choice of inertial frame must be made.
2) The above correspondence of clock readings is meaningful only in the home frame. When the travel reads one of the distance home clocks, he cannot conclude that this is the "current" reading on the home clock in his own frame. Remote clocks have different readings in different frames.
3) This comparison of clocks is possible because space is flat in SR and the home clock remains at rest in the same inertial frame. In more general cases such simple comparison of clocks may not be possible.
4) Einstein has analyzed this paradox using the acceleration and distance of the traveler at turn around. He claimed that, during turn around, the home clock (at home) runs much faster than the travelers clock due to the distance and the degree of the traveler's acceleration.
Question:
At least superficially, 4) is in conflict with the claim that "acceleration does not affect clock rates". Has anyone seen an analysis that demonstrates an equivalence of the two approaches? Otherwise can someone clarify why acceleration does not affect relative clock rates, while Einstein appears to claim it does?
Beginners, like myself, when confronting the twin paradox often want to know where it is that the traveling twin loses so much time. A frustrated poster trying to explain the paradox posted this:
He's been given many answers and he rejects every one because he wants an answer that fits his preconceived notion that the traveling twin's clock must lose time at a particular point in the trip.
Still, the beginner is persistent in wanting to know where these clocks differ along the trip and by how much. There is no single answer due to the relativity of simultaneity but there are some approaches.
To answer this question, one approach is to explain what each twin sees (e.g. with a powerful telescope) on the other's clock. In this case a Doppler effect occurs in the clocks readings due to relative motion. Thus this description of the relationship between the clocks has a complicating factor: the delays in the readings by each twin of the other's clock are changing due to the the changing distance between the twins.
But there is another way of viewing the relationship between the clocks.
In the simple twin paradox, one twin stays at home and the other travels to a distant destination and back again at a substantial fraction of the speed of light. We can assume that the traveling twin accelerates to a fixed speed almost instantaneously when he leaves, when he turns around and that he stops quickly when he returns home. The traveling twin moves with constant velocity on the long outbound and inbound legs of the journey.
With this scenario in mind, here's another clock comparison method:
Prior to the trip, a number of clocks are placed at intervals along the path that the traveler will take to the destination.
All of these clocks along the path to the destination are placed so that they are stationary wrt the home clock. That is, all these clocks are at rest in the same inertial frame with the home clock.
Using Einstein's clock synchronization method, we synchronize all of these clocks with the home clock.
The clocks along the traveler's path then represent "home clock time" in the home clock's inertial frame. Since this frame is inertial throughout the trip we know that the established synchronization of these clocks with the home clock persists throughout, in the home frame.
The traveler can read these distributed "home clocks" during his trip and compare them with the readings with his own clock. Then he has an answer to how and where he is losing time relative to the home clock. The comparison is illustrated in this diagram linked from http://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters_2013_Jan_1/spacetime_tachyon/index.html (sorry for the size):
Copyright John D. Norton. January 2001, September 2002; July 2006; February 3, 2007; January 23, September 24, 2008; January 21, 2010; February 1, 2012.
In the diagram the rocket twin travels at 86.6% the speed of light resulting in a time dilation factor of 1/2. The straight vertical path is the home clock's path over time (the home clock's worldline). The dogleg is the traveler's worldline. Each is marked with the proper time in years on each of the twin's clocks. The horizontal planes show the positions of the home clocks (imagine the line of clocks) and of the traveler at different times in the home frame.
The travel reads the "home time" using the clocks placed along the plane. The traveler finds the following correspondence between home time and the time on the own clock (as shown in the diagram):
Clock readings in years
Home Traveler
0 0
2 1
4 2
6 3
8 4
When the traveler returns he can show the home twin the above record, so the home twin can know in his own frame how old the traveler was when he was a certain age.
There is no mystery about where these clocks get out of sync from this perspective. They do it uniformly along the entire trip.
Acceleration does not directly affect the clocks, it is the speed of the traveler and the time over which he travels with that speed that determines the age gap. The above clock comparison exactly reflects the time dilation of the traveling twin which is constant throughout the trip.
Note that the traveling twin could, instead of traveling far away, make small circles around home at the same speed for the same amount of time and the clock results would be the same. So it appears that it has little to do with how far away he travels.
Acceleration does not affect the age difference directly but the acceleration is necessary to follow any non-straight path through flat spacetime.
The twin paradox is "why can't we just reverse the role of the home and traveler in the diagram, such that the traveler is considered stationary and the home clock is considered to move, so that the traveler gets older instead"? We cannot because the traveler's path through spacetime cannot be made a straight line in any such diagram. It is a dogleg in all inertial frames, while the path of the home clock is straight in all inertial frames.
Caveats:
1) There is no unique way to compare the clock readings, some choice of inertial frame must be made.
2) The above correspondence of clock readings is meaningful only in the home frame. When the travel reads one of the distance home clocks, he cannot conclude that this is the "current" reading on the home clock in his own frame. Remote clocks have different readings in different frames.
3) This comparison of clocks is possible because space is flat in SR and the home clock remains at rest in the same inertial frame. In more general cases such simple comparison of clocks may not be possible.
4) Einstein has analyzed this paradox using the acceleration and distance of the traveler at turn around. He claimed that, during turn around, the home clock (at home) runs much faster than the travelers clock due to the distance and the degree of the traveler's acceleration.
Question:
At least superficially, 4) is in conflict with the claim that "acceleration does not affect clock rates". Has anyone seen an analysis that demonstrates an equivalence of the two approaches? Otherwise can someone clarify why acceleration does not affect relative clock rates, while Einstein appears to claim it does?