aforl
- 1
- 0
Studying for a test, and this problem stumped me because of the confusing nature of the question... Not sure where radiation shld come into play. Any help appreciated! THANKS!
1. Homework Statement
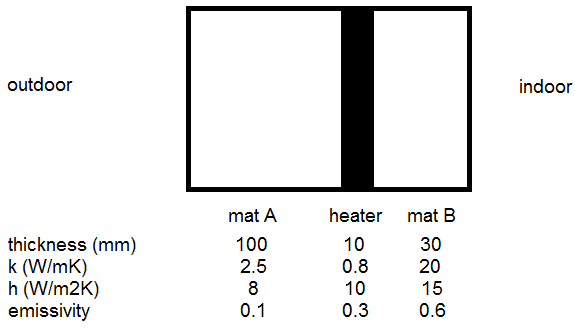
The walls of an apartment are made of two layers of mat with a heater layer in between.
Thickness, thermal conductivity, emissivity of each surface and convective heat transfer coefficient in still air are given above.
The outdoor temperature is at -10oC, and the indoor temperature is controlled by the heater layer.
Assume the apartment has 4 side walls, each 10m wide and 3m high, and heat loss through ceiling and ground are ignored.
Also assume inner surface of the wall (facing indoor) are perfectly insulated, but do not assume convection and radiation at outer surface is negligible.
(a) Sketch the (steady-state) temperature profile across the wall, from the outer surface to the inner surface.
(b) The heater is generating heat at 250W/m2. What is the steady state temperature of the Mat B layer? To estimate the radiation heat transfer coefficient at the outer surface of the wall, assume temperature at surface of Mat A is close to -10oC.
2. Equations
Conduction across plane (without heat generation):
q=kAΔT/L
T(x) = Tsurface1 - ΔTx/L
Rt = L/kA
Conduction across plane (with heat generation):
d2T/dx2 + q/k = 0
T(x) = T(x) = Tsurface1 + qL2/2k (1 - x2/L2)
Thermal Resistance
Rconv = 1/hA
Rrad = 1/εσA(Ts + Tsur)(Ts2+Tsur2)
(a) Assume temperature within heater layer is constant (can I do so?),
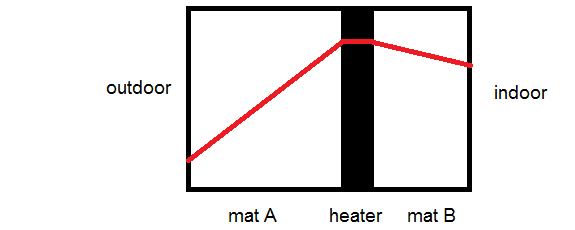
I drew them linear because without heat generation, the profile is linear. The slope in mat A is also steeper due to the k/L ratio compared to mat B. (Is this alright?)
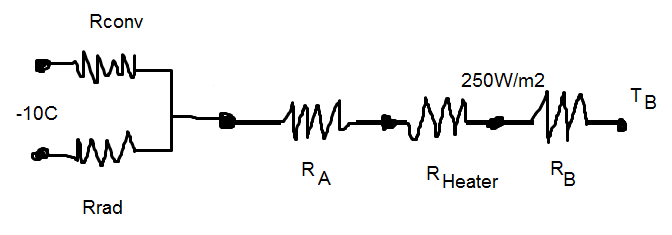
(b) So to solve this, I drew a thermal circuit. However I'm not sure where to place the radiation resistance. Please help me verify if I drew this correctly.
The question says assume surface of A is -10C, wouldn't that means no radiation and convection?
Please help! Any help appreciated thanks so much !
1. Homework Statement
The walls of an apartment are made of two layers of mat with a heater layer in between.
Thickness, thermal conductivity, emissivity of each surface and convective heat transfer coefficient in still air are given above.
The outdoor temperature is at -10oC, and the indoor temperature is controlled by the heater layer.
Assume the apartment has 4 side walls, each 10m wide and 3m high, and heat loss through ceiling and ground are ignored.
Also assume inner surface of the wall (facing indoor) are perfectly insulated, but do not assume convection and radiation at outer surface is negligible.
(a) Sketch the (steady-state) temperature profile across the wall, from the outer surface to the inner surface.
(b) The heater is generating heat at 250W/m2. What is the steady state temperature of the Mat B layer? To estimate the radiation heat transfer coefficient at the outer surface of the wall, assume temperature at surface of Mat A is close to -10oC.
2. Equations
Conduction across plane (without heat generation):
q=kAΔT/L
T(x) = Tsurface1 - ΔTx/L
Rt = L/kA
Conduction across plane (with heat generation):
d2T/dx2 + q/k = 0
T(x) = T(x) = Tsurface1 + qL2/2k (1 - x2/L2)
Thermal Resistance
Rconv = 1/hA
Rrad = 1/εσA(Ts + Tsur)(Ts2+Tsur2)
The Attempt at a Solution
(a) Assume temperature within heater layer is constant (can I do so?),
I drew them linear because without heat generation, the profile is linear. The slope in mat A is also steeper due to the k/L ratio compared to mat B. (Is this alright?)
(b) So to solve this, I drew a thermal circuit. However I'm not sure where to place the radiation resistance. Please help me verify if I drew this correctly.
The question says assume surface of A is -10C, wouldn't that means no radiation and convection?
Please help! Any help appreciated thanks so much !