NathanRB
- 4
- 0
- Homework Statement
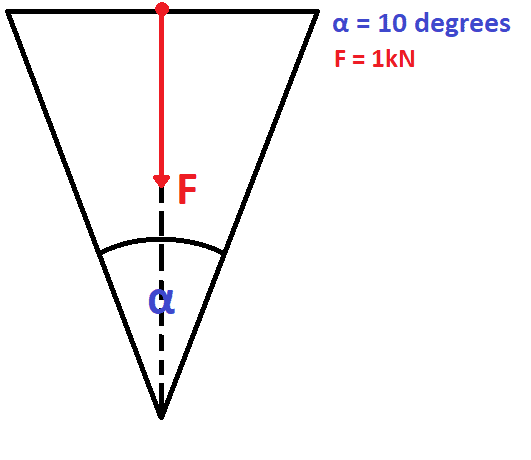
- Which force acts perpendicular to the side faces of an axe head, if this axe head encloses an angle of 10 degrees (the sharpness of the axe, so to say), and a force of 1000N is acted on the back of the axe head as it cuts through a piece of wood.
- Relevant Equations
- Fk = F * sin (0.5 α)
Fx = Fk * cos (0.5 α)
Description:
F: Force acted on the back of the axe head
Fx: horizontal force
Fk: Force acting perpendicular to each of the side faces of the axe head
α: angle enclosed by the two side faces of the axe = 10 degrees
Say that these pictures are accurate.
 Personally, I think I can solve this problem, but the issue is, that I had a debate on it with my Physics teacher.
Personally, I think I can solve this problem, but the issue is, that I had a debate on it with my Physics teacher.
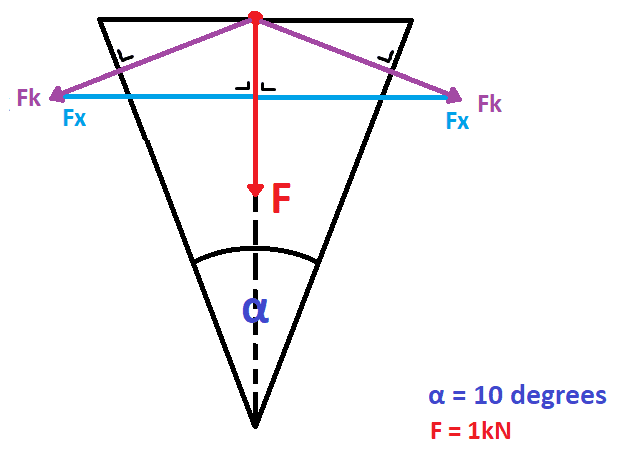 This is how my teacher would solve it; my teacher says that each Fk on each side is constructed from half of F and Fx. So, F = 2 * Fk * sin (0.5 α), hence Fk = F / (2 * sin (0.5 α)) and Fx = Fk * cos (0.5 α).
This is how my teacher would solve it; my teacher says that each Fk on each side is constructed from half of F and Fx. So, F = 2 * Fk * sin (0.5 α), hence Fk = F / (2 * sin (0.5 α)) and Fx = Fk * cos (0.5 α).
The question is actually to find the force acting perpendicular to the faces, but for some reason, my teacher went and calculated Fx instead of just calculating Fk. That is not the issue, however.
My issue with this is, as the angle α approaches 0, the Force Fk and also Fx approaches infinity. I presented this fact and my teacher said that as the angle becomes closer, the equation doesn't apply anymore because if the angle is so small, it wouldn't be an axe anymore, and rather, a knife, and we would need another equation for that. I personally think that explanation makes absolutely no sense.
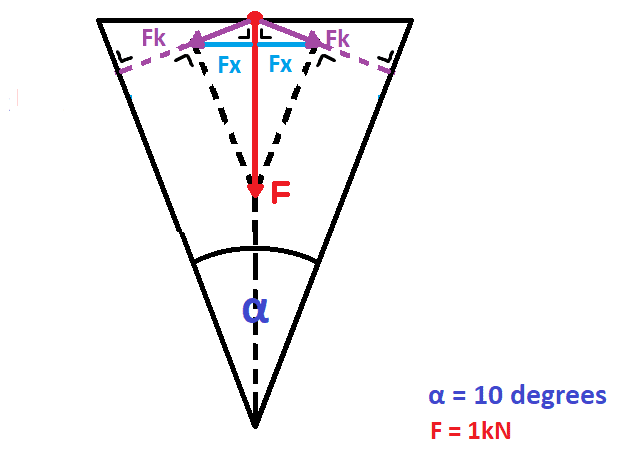 This is actually how I would solve it. I think that Fk and Fx are components of F. So, Fk = F * sin (0.5 α) but still, Fx = Fk * cos (0.5 α). I think it's the right way to go, but I'm here because I'm open to any explanation. If I am wrong, please do explain why or how. If my teacher's method is wrong, it would be great if more than one person, would be willing to give their opinions (so it would be enough to convince my teacher). And if both methods are wrong, please provide the correct method and explanation. Thank you!
This is actually how I would solve it. I think that Fk and Fx are components of F. So, Fk = F * sin (0.5 α) but still, Fx = Fk * cos (0.5 α). I think it's the right way to go, but I'm here because I'm open to any explanation. If I am wrong, please do explain why or how. If my teacher's method is wrong, it would be great if more than one person, would be willing to give their opinions (so it would be enough to convince my teacher). And if both methods are wrong, please provide the correct method and explanation. Thank you!
The question is actually to find the force acting perpendicular to the faces, but for some reason, my teacher went and calculated Fx instead of just calculating Fk. That is not the issue, however.
My issue with this is, as the angle α approaches 0, the Force Fk and also Fx approaches infinity. I presented this fact and my teacher said that as the angle becomes closer, the equation doesn't apply anymore because if the angle is so small, it wouldn't be an axe anymore, and rather, a knife, and we would need another equation for that. I personally think that explanation makes absolutely no sense.