Blugga
- 22
- 0
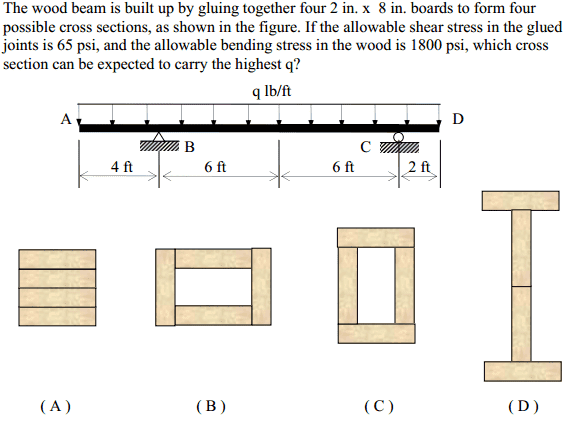
Which wood cross sectioπ caπ carry hïghest uπiform load
Moment of inertia for rectangle I=(1/12)bh3
τ=(VQ)/(I*b)
σ=(MV)/I
I started by finding reactions at B and C
Then drew the sheer and moment diagrams (to save space i made it a link)
http://oi47.tinypic.com/qsmkxh.jpg
To find which cross section can withstand the biggest q, I found the moment of inertia about the z axis (neutral axis) for each figure.
(A)Iz=2*{((1/12)*8*23)+[(2*8)*32]}+2*{((1/12)*8*23)+[(2*8)*12]}
Iz=341.33 in4
(B)Iz=2*{((1/12)*8*23)+[(2*8)*32]}+2*{((1/12)*2*83)}
Iz=469.33 in4
(C)Iz=2*{((1/12)*8*23)+[(2*8)*52]}+2*{((1/12)*2*83)}
Iz=981.33 in4
(D)Iz=2*{((1/12)*8*23)+[(2*8)*92]}+2*{((1/12)*2*83)+[(2*8)*42]}
Iz=3285.33 in4
Because both of the equations I posted for τ and σ are dependent on Inertia, I figured since that when solving for (q) we would have to multiply by Inertia so whichever cross section has the biggest Inertia will also have a bigger (q). Therefore, cross section (D) was the pick. Was I right to assume this?
τmax=[(6.5q)*Q(0)]/[3285.33*2]=65; where Q(0)=208. not sure about that value
∴q=315 lb/ft
σmax=[(34.125lb-ft)(12in/ft)q*10]/3285.33=1800
∴q=1444.10 lb/ft and so the max q can be is 315 lb/ft
This is my first attempt so any help is appreciated.
Homework Statement
Homework Equations
Moment of inertia for rectangle I=(1/12)bh3
τ=(VQ)/(I*b)
σ=(MV)/I
The Attempt at a Solution
I started by finding reactions at B and C
Then drew the sheer and moment diagrams (to save space i made it a link)
http://oi47.tinypic.com/qsmkxh.jpg
To find which cross section can withstand the biggest q, I found the moment of inertia about the z axis (neutral axis) for each figure.
(A)Iz=2*{((1/12)*8*23)+[(2*8)*32]}+2*{((1/12)*8*23)+[(2*8)*12]}
Iz=341.33 in4
(B)Iz=2*{((1/12)*8*23)+[(2*8)*32]}+2*{((1/12)*2*83)}
Iz=469.33 in4
(C)Iz=2*{((1/12)*8*23)+[(2*8)*52]}+2*{((1/12)*2*83)}
Iz=981.33 in4
(D)Iz=2*{((1/12)*8*23)+[(2*8)*92]}+2*{((1/12)*2*83)+[(2*8)*42]}
Iz=3285.33 in4
Because both of the equations I posted for τ and σ are dependent on Inertia, I figured since that when solving for (q) we would have to multiply by Inertia so whichever cross section has the biggest Inertia will also have a bigger (q). Therefore, cross section (D) was the pick. Was I right to assume this?
τmax=[(6.5q)*Q(0)]/[3285.33*2]=65; where Q(0)=208. not sure about that value
∴q=315 lb/ft
σmax=[(34.125lb-ft)(12in/ft)q*10]/3285.33=1800
∴q=1444.10 lb/ft and so the max q can be is 315 lb/ft
This is my first attempt so any help is appreciated.
Last edited: