matematikuvol
- 190
- 0
f(t)=\int^{c+i\infty}_{c-i\infty}F(s)e^{st}ds
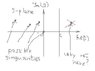
Why we suppose that all singularities are left from line Re(s)=c?
Why we suppose that all singularities are left from line Re(s)=c?