cwill53
- 220
- 40
- Homework Statement
- An electric lamp weighing 5lbs is suspended by a cord AB from the ceiling and pulled towards the wall by the cord BC. Determine the tensions ##T_{A}## in the cord AB and ##T_{C}## in the cord BC if the angles ##\alpha## and ##\beta## are ##60^{\circ}## and ##135^{\circ}##, respectively. Neglect the weight of the cords.
Ans. ##T_{A}##= 3.65 lbs ##T_{C}##==2.6 lbs
- Relevant Equations
- $$\sum \vec{F}=m\vec{a}$$
I had made equations for the forces in the x-direction and y-direction, but when solving them they yielded the wrong answers, which makes me think that they were incorrect:##(T_{A}cos60^{\circ}+T_{C}cos45^{\circ})=0##
##(T_{A}sin60^{\circ}+T_{C}sin45^{\circ})=5lbs##
Here's the diagram for the problem:
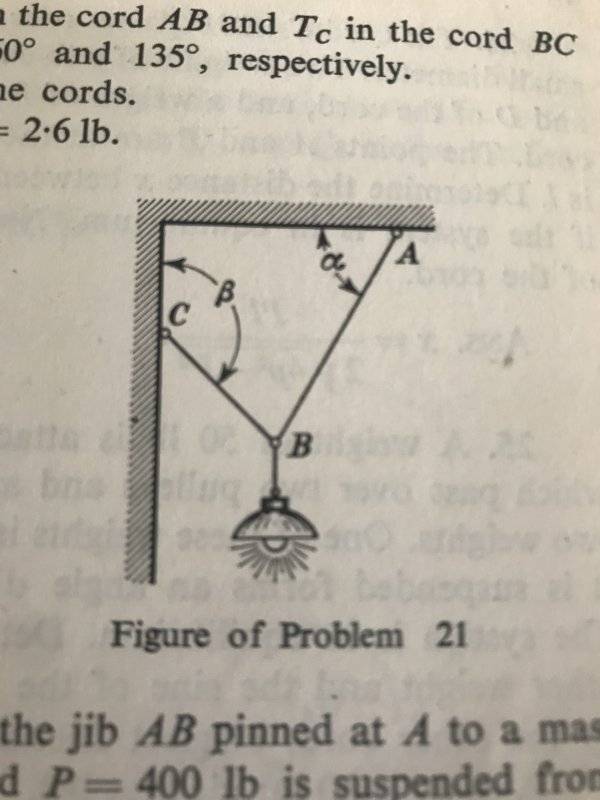
##(T_{A}sin60^{\circ}+T_{C}sin45^{\circ})=5lbs##
Here's the diagram for the problem:
Last edited: