1/2"
- 98
- 0
Homework Statement
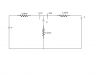
In the given circuit find the current i1,i2,i3.
(Image of the circuit is attached)
Homework Equations
current=(emf)/total resistance
The Attempt at a Solution
The original question actually asks me to find the currents using Kirchoff's laws .Since I feel this method to be a little tedious I tried to do it another way.
But the problem is the answers are not coming correct this way ,(which is as follows )
First since the two cells are connected opposite to each other i have assumed the resultant emf of the 21V to be 4V and I have neglected the other 17V cell.
then considering 2Ω and 5Ω resistances to be parallel to each other their resultant comes to be
(10/7)Ω .And this one being in series with 3Ω, The final resistance of the circuit comes out to be
(31/7)Ω.
Accordingly current should be i1=28/31 A
I am going seriously wrong somewhere , but can't figure out where.
 .
.Can you please help?
Thanks in advance!
Attachments
Last edited: