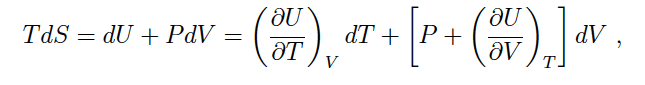Why can U be expanded in terms of T and V?

  • Context: Undergrad 
  • Thread starter Thread starter thegirl
  • Start date Start date
  • Tags Tags
    Terms
Click For Summary
SUMMARY

The discussion focuses on the expansion of internal energy (U) in terms of temperature (T) and volume (V) when expressing the differential of entropy (dS). The mathematical relationship is defined by the equation dU/dT(V) + dU/dV(T), which represents the total differential of U with respect to the coordinates (T, V). This expansion does not alter the meaning of the expression, as it adheres to the principles of thermodynamics. The conversation also touches on the number of intensive properties necessary to define the state of a single-phase material with constant composition.

PREREQUISITES
  • Understanding of thermodynamic principles
  • Familiarity with the concepts of internal energy (U), temperature (T), and volume (V)
  • Knowledge of differential calculus in the context of thermodynamics
  • Basic grasp of intensive and extensive properties in materials science
NEXT STEPS
  • Study the derivation of the first law of thermodynamics
  • Learn about the Maxwell relations in thermodynamics
  • Explore the concept of state functions and their differentials
  • Investigate the role of intensive properties in phase equilibrium
USEFUL FOR

Students and professionals in thermodynamics, materials science researchers, and anyone interested in the mathematical foundations of energy transformations in physical systems.

thegirl
Messages
40
Reaction score
1
when expressing dS as a function of dV and dT, dU was expanded out as you can see in the screenshot below, is there a mathematical rule which allows this? does the fact that the internal energy is expanded out change the meaning of the expression?
Screen Shot 2016-03-24 at 17.45.17.png
 
Science news on Phys.org
How many intensive properties are required to specify the state of a single phase material of constant composition?
 
thegirl said:
when expressing dS as a function of dV and dT, dU was expanded out as you can see in the screenshot below, is there a mathematical rule which allows this? does the fact that the internal energy is expanded out change the meaning of the expression?View attachment 97881
dU/dT(V)+dU/dV(T) is the differential of U with the coordinated (T,V)
 
  • Like
Likes   Reactions: thegirl
Thank you!
 

Similar threads

Undergrad How Does Temperature Affect Wire Tension at Constant Length?
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad The far reaching ramifications of the work-energy theorem
  • · Replies 31 ·
2
Replies
31
Views
4K
Undergrad How did Hamilton derive the characteristic function V in his essay?
  • · Replies 3 ·
Replies
3
Views
1K
Undergrad Taking Derivatives of the Fundamental Property Relations
  • · Replies 10 ·
Replies
10
Views
1K
Chemistry Why can we differentiate this entropy total derivative with repect to Temperature?
  • · Replies 5 ·
Replies
5
Views
4K
Question about the derivation of Exact Differentials in thermo
  • · Replies 4 ·
Replies
4
Views
1K
Irodov 1.23 confusion: Calculate distance traveled and time elapsed for this decelerating particle
  • · Replies 2 ·
Replies
2
Views
1K
Undergrad How to develop the rocket equation?
  • · Replies 47 ·
2
Replies
47
Views
4K
Undergrad First law of thermodynamics -- two different expressions for dQ
  • · Replies 23 ·
Replies
23
Views
3K
Graduate Question about u and h and Its Differential Changes for Ideal Gases
  • · Replies 10 ·
Replies
10
Views
2K