tzhu
- 3
- 0
I tried to do this pendulum problem with force analysis, but I kept getting a wrong answer. Eventually I figured it out using torque, but I still have no clue why I was getting a wrong answer when I try to use f=ma. Any help appreciated!
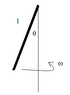
A conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity \omega (the upper end of the rod is hinged). Find the angle \theta between the rod and the vertical.
Here's my original attempt:
From vertical equilibrium, we have
F\cos{\theta}=mg
From the centripetal force, looking at each mass dm, we have
dF\sin{\theta}=\omega^2 x \sin{\theta} dm, or
dF=\omega^2 x (\frac{m}{l}) dx
Integrating from zero to l,
F=\frac{1}{2} \omega^2 lm
equating with the F in the first equation, I got
\cos{\theta}=\frac{2g}{\omega^2 l}, which is wrong.
But I can get the right answer when I solve it with equilibrium/torque analysis in the rotating frame, which turns out to be \frac{3g}{2 \omega^2 l}
Can anyone point out what is wrong with my solution? It's been bothering me forever!
Homework Statement
A conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity \omega (the upper end of the rod is hinged). Find the angle \theta between the rod and the vertical.
The Attempt at a Solution
Here's my original attempt:
From vertical equilibrium, we have
F\cos{\theta}=mg
From the centripetal force, looking at each mass dm, we have
dF\sin{\theta}=\omega^2 x \sin{\theta} dm, or
dF=\omega^2 x (\frac{m}{l}) dx
Integrating from zero to l,
F=\frac{1}{2} \omega^2 lm
equating with the F in the first equation, I got
\cos{\theta}=\frac{2g}{\omega^2 l}, which is wrong.
But I can get the right answer when I solve it with equilibrium/torque analysis in the rotating frame, which turns out to be \frac{3g}{2 \omega^2 l}
Can anyone point out what is wrong with my solution? It's been bothering me forever!
Last edited: