cherrios
- 8
- 0
I've worked this problem out, but I seem to get zero force on the second dipole due to the first dipole.
The problem is situated as such:
There are Q charges along the y axis: Q+ and Q-. They are a distance r apart. Their distance from the origin (at the center of the two charges) is r/2. This is the first dipole.
The second dipole is on the the x-axis, to the right. These have charges q+ and q-. The distance q+ has from the origin is x-d/2, for q-, the distance is x+d/2. (q+ and q- are a distance 'd' apart).
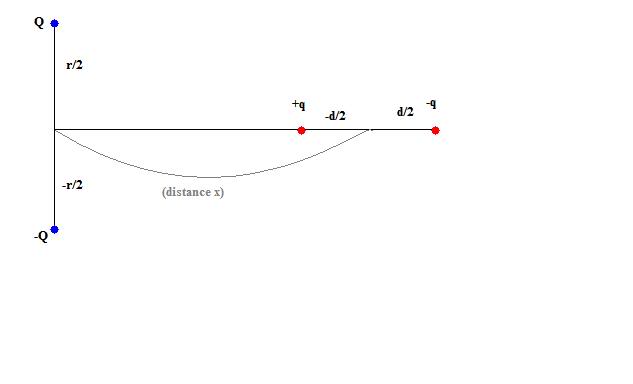
I took the force on each q+ and q- charge by Q+ and Q-. I took the tangent as the distance between them, but I seem to get zero.
Also, how would torque on one dipole due to another be calculuated?
The problem is situated as such:
There are Q charges along the y axis: Q+ and Q-. They are a distance r apart. Their distance from the origin (at the center of the two charges) is r/2. This is the first dipole.
The second dipole is on the the x-axis, to the right. These have charges q+ and q-. The distance q+ has from the origin is x-d/2, for q-, the distance is x+d/2. (q+ and q- are a distance 'd' apart).
I took the force on each q+ and q- charge by Q+ and Q-. I took the tangent as the distance between them, but I seem to get zero.
Also, how would torque on one dipole due to another be calculuated?