Michele Nunes
- 42
- 2
Homework Statement
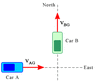
The drawing shows two cars traveling in different directions with different speeds. Their velocities are:
vAG = velocity of car A relative to the Ground = 27.0 m/s, due east
vBG = velocity of car B relative to the Ground = 21.0 m/s, due north
The driver of car B looks out the window and sees car A. The velocity of car A relative to car B is vAB. The angle that the velocity vAB makes with respect to due east is?
Homework Equations
The Attempt at a Solution
I got the correct angle which is 37.9 degrees, however the answer says 37.9 degrees south of east. HOW IS IT SOUTH OF EAST?? I'm so confused, why is it not north of east? The angle is made by going 37.9 degrees NORTH of the horizontal east axis so why in the world is the answer south of east, I just do not understand.