Here is a table for wire gauge (AWG) and Ohms (resistance) per 1000 feet. The only columns you need to worry about are the first and third. You can see that 1000 feet of a 22 gauge wire has a resistance of 16.0 Ohms. I would say a good estimate for the length of your wire is 1 foot. This gives a total resistance for your 22 gauge wire of 0.016 Ohms:
{\frac{16.0 \, Ohms}{1000 \, feet}} = 0.016 \, Ohms.
Source: http://www.picwire.com/technical/wire.php
Quickly, you can see that the shorter the wire, the lower the resistance (and vice versa).
Also, the larger gauge the wire, the lower the resistance of the wire (a 10 AWG wire is actually
larger than a 22 AWG wire - compare the wire diameters in the table to confirm this).
So now we understand the wire resistance. Let's do Ohm's law (V = IR). I'll draw out three of your circuits and calculate the current (I) and voltage (V) for each component and node in the circuit. Each node will be a solid color. Example, RED = 9 Volts at every point, Green = 0 Volts at every point.
Ohm's Law is quite simple:
V = I \times R
or
Voltage = Current \times Resistance
The unit of Voltage is Volts. The unit of Current is Amperes (Amps). The unit of Resistance is Ohms.
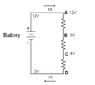
Okay, let's look at your first circuit with an ideal 9 Volt battery (ignoring the internal resistance for simplicity). The LED is represented as R1, a 300 Ohm Resistor.
We already know the voltage across R1: 9 Volts.
We also know the resistance of R1 since it's the equivalent of your LED: 300 Ohms
The only thing we need to calculate is the current going through R1.
Using Ohm's Law:
V = I \times R,
9 = I \times 300,
I= 0.03 \, Amps
Pretty simple then. Your LED has 0.03 Amps going through it. That is what is necessary for the LED to produce light.
Next let's look at the exact same circuit except we'll treat the battery more realistically and give it an internal resistance of 4.5 Ohms. So the battery is now represented by V1 + R2.
Now we have two resistors in series (R2 & R1). Resistors in series can be added together to calculate the current (Current flows in a loop - the current through R2
must be the same as the current through R1). We want to see how much current is
really going through the LED (R1) with a more realistic 9 Volt battery.
We know there is 9 Volts across R2+R1.
We know R2 = 4.5 Ohms.
We know R1 = 300 Ohms.
V = I \times R,
9 = I \times (4.5 + 300),
9 = I \times 304.5,
I= 0.0296 \, Amps
So we see with a bit more realistic circuit, your LED has 0.0296 Amps going through it. Not too different from the ideal 9 Volt battery. We can also use this current to calculate the Voltage across the LED (R1).
V_{R1} = I \times R_{R1},
V_{R1} = 0.0296 \times (300),
9 = I \times 304.5,
V_{R1} = 8.88 \, Volts
We can already see a little bit of a voltage drop when considering the battery's series resistance.
Last, we'll add the 22 AWG wire across the battery. The wire is shown as R3 with a resistance of 0.016 Ohms. In order to calculate the current through R1, we'll need to do some work with series resistors and parallel resistors. This is a bit more complex, but trust that we'll be getting correct numbers at the end (unless peers find errors in my math). I1 = I_{R1}, etc.
First we add R1 and R3 as parallel resistors to get an equivalent of the two:
{\frac{1}{R_{eq}}} = {\frac{1}{R1}}+{\frac{1}{R3}},
{\frac{1}{R_{eq}}} = {\frac{1}{300}}+{\frac{1}{0.016}},
R_{eq} = 0.015999 \, Ohms
So R_{eq} of R1 and R3 is just slightly smaller than R3. Now we need to add this to R2 in order to get the total equivalent resistance.
R_{tot}= R2+R_{eq},
R_{tot}= 4.5+0.015999,
R_{tot}= 4.515999,
Then we can find the current through R2 (this is
only the current through R2 since the current splits between R3 and R1 before returning to the battery and completing the loop).
V = I_{R2} \times R_{tot},
9 = I_{R2} \times 4.515999,
I_{R2}= 1.992915 \, Amps
With the current going through R2 we can now use Ohm's Law again to find the voltage drop across R2. This will let us find the Voltage across R1 and R3 and then finally get the current through R1 (LED).
V_{R2} = I_{R2} \times R2,
V_{R2} = 1.992915 \times 4.5,
V_{R2}= 8.96812 \, Volts
That's a hell of a voltage drop across R2. Remember R2 is the battery's series resistance. It's internal to the 9 Volt battery. The voltage you really end up seeing on the outside of the battery is:
V_{R1} = V - V_{R2},
V_{R1} = 9 - 8.96812,
V_{R1}= 0.03188\, Volts
So the voltage across R1 (LED) is only 0.03188 Volts (The voltage across the wire R3 is the exact same as the voltage across R1, 0.03188 Volts. This is because they are both between the same nodes, or potentials).
Let's finish up with the current through R1:
V_{R1} = I_{R1} \times R1,
0.03188 = I_{R1} \times 300,
I_{R1}= 0.00010627 \, Amps
The current through your LED is 0.00010627 Amps in this case (versus around 0.03 Amps when the LED produced light). Where's the rest of the current? Through the wire:
V_{R3} = I_{R3} \times R3,
0.03188 = I_{R3} \times 0.016,
I_{R3}= 1.9925 \, Amps
If any of this is confusing, these search terms should help you find more explanation:
Ohm's Law
Adding Series Resistors
Adding Parallel Resistors
Resistive Voltage Divider
I would also highly recommend looking at Water/Circuit Analogies. The flow of electricity is very analogous to the flow of water. There's probably plenty of videos/sites that will help make electricity (and basic components like resistors) more visibly understandable. Here's a good one:
http://www.physics-chemistry-intera...raulic_analogy_difference_voltage_current.htm On the last side they use the term "INTENSITY" instead of "CURRENT." I'm not sure why but it should be seen as the same thing.
A few notes:
A resistor is not the real equivalent of an LED but for this purpose a resistor serves just fine. Be aware that an LED has polarity, where a resistor doesn't.
From start to finish rounding changed significantly - this was only necessary because of such low current values. I should have used more consistent rounding.
There's quicker ways to solve for the values in Circuit 3 but I tried to keep it simple.
Wires are not typically analyzed as resistors in this type of circuit (rather, they are modeled as having 0 resistance). For very long wire/cable runs, resistance is considered (and possibly short runs for high frequency use, but I know less about that). Wires are just copper and your breadboard connections are all through copper (or some similarly conductive material). Adding the 22 AWG jumper does the same thing as plugging both battery leads into the same rail of the breadboard (short circuit, imagine V = IR except R = 0, V = 9).
I hope this was helpful.