haribol
- 52
- 0
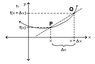
In the attached picture, the equation for the limit I think is:
\lim_{\Delta x \rightarrow 0} \\\ \frac{f(x+ \Delta x) - f(x)}{\Delta x}
When \Delta x approaches 0, why wouldn't the f(x+ \Delta x) approach f(x)? Because as the point Q approaches P, then wouldn't the y value of point Q also approach that of P? Or am I not understanding the concept?
\lim_{\Delta x \rightarrow 0} \\\ \frac{f(x+ \Delta x) - f(x)}{\Delta x}
When \Delta x approaches 0, why wouldn't the f(x+ \Delta x) approach f(x)? Because as the point Q approaches P, then wouldn't the y value of point Q also approach that of P? Or am I not understanding the concept?