- #1
FocusedWolf
- 81
- 0
I have a function that is not giving me critical points for where their appears to be a maximum.
from plot their seems to be a cp at approximately x=y=5
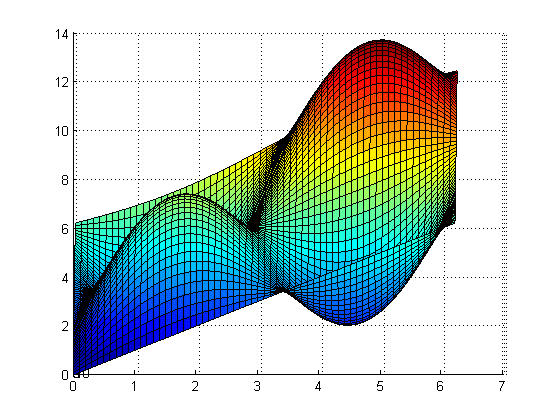
However, these are the cp's:
cpx =
-0.2618
-1.3090
1.8326
2.8798
-2.8798
-1.8326
1.3090
0.2618cpy =
-0.2618
-1.3090
1.8326
2.8798
0.2618
1.3090
-1.8326
-2.8798
When evaluated on the boundry [0,2pi]x[0,2pi] F(0,0)=0 as a absolute minimum and F(2*pi, 2*pi)=12.5664 as absolute maximum...even though in the graph... 2*pi is lower then the imaginary big red mountain on right...for which their seems to be no cp...
Here's code that generates plot and finds critical points
So my question is...is their a cp at that red mountain? or is their no red mountain :P
They say when fx and fy DNE their is also cp...but i don't see that happening since fx and fy are polynomials...
from plot their seems to be a cp at approximately x=y=5
However, these are the cp's:
cpx =
-0.2618
-1.3090
1.8326
2.8798
-2.8798
-1.8326
1.3090
0.2618cpy =
-0.2618
-1.3090
1.8326
2.8798
0.2618
1.3090
-1.8326
-2.8798
When evaluated on the boundry [0,2pi]x[0,2pi] F(0,0)=0 as a absolute minimum and F(2*pi, 2*pi)=12.5664 as absolute maximum...even though in the graph... 2*pi is lower then the imaginary big red mountain on right...for which their seems to be no cp...
Here's code that generates plot and finds critical points
Code:
%plotting it
[x,y] = meshgrid(0 : .1 : 2*pi)
z = x+y+4.*sin(x).*sin(y)
surf(x,y,z)
%contour(x,y,z,20); axis square; colorbar;
syms x y
f = x+y+4*sin(x)*sin(y)
fx = diff(f,x)
fxx = diff(fx,x)
fy = diff(f,y)
fyy = diff(fy,y)
fxy = diff(fx,y)
d = fxx*fyy-fxy^2
% Solve for all critical points of f using solve
[cpx,cpy] = solve(fx,fy)
% Make critical points decimals
cpx = double(cpx)
cpy = double(cpy)
% Make inline functions for f, fxx, and d
F = inline(vectorize(f),'x','y')
D = inline(vectorize(d),'x','y')
Fxx = inline(vectorize(fxx),'x','y')
% define boundries
%[0 0; 0 2*pi; 2*pi 0; 2*pi 2*pi]
boundx = [0; 0; 2*pi; 2*pi]
boundy = [0; 2*pi; 0; 2*pi]
% Make a table of the cp's, F(at cp's), D(at cp's), and Fxx(at cp's)
T = [cpx cpy F(cpx,cpy) D(cpx,cpy) Fxx(cpx,cpy)]
%Evaluate F at boundries of region [0,2pi]x[0,2pi]
T = [boundx boundy F(boundx,boundy)]So my question is...is their a cp at that red mountain? or is their no red mountain :P
They say when fx and fy DNE their is also cp...but i don't see that happening since fx and fy are polynomials...
Last edited: