Why is (not) the resulting unit of this equation rad/s ?

[hackYou]

Hi guys,
My first time here. Looks like a nice forum with friendly members.

I have a question. I'm kinda confused by this (and I know it's a shame since I'm on my third year University, almost making my degree).

What I remember from my kinematics/dynamics classes this (or similar) equation always yielded the result in rad/s but now I'm stuck here. I can't justify it using SI units. What I get as output is 1/s which as much as I know is the Hz. Meaning 1 revolution per second and not 1 radian per second.

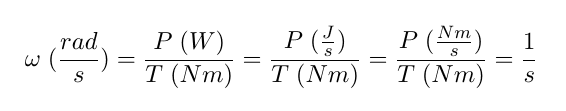
If anyone could chime in and clarify this for me would be nice.
Thank you in advance.

P.S. My first time here. I didn't know how to insert math equations so I inserted a picture. If this is somehow against the site rules or in the wrong place feel free to remove it or tell me and I'll do it myself.

 

[BiGyElLoWhAt]

That's the funny thing about radians. They're not actually units, they're counters, and they're unitless. Sometimes they just come and go as they please, or so it seems. Hz and rad/s are very similar units. If you think about Hz, it's hits/second, or counters/second. Every time your device registers a hit, it adds one and after one second, you have your hz value. If you're talking angular velocity, it's also a counter, it's essentially how many revolutions/second, but using the radius of a circle as the distance between the counters. I suppose the fundamental difference between the two would be that rad/s uses a specific counter, i.e. radians, and Hz is more general. You could readily measure angular velocity in Hz, just pick a spot on the circle, count how many times that your object rotates within the circle, and divide that by the time lapse. That will give you times/second, which, since times isn't actually a unit, it's really 7/second or whatever.

I hope that helped.

Welcome to PF by the way.

 

[Hesch]

What I get as output is 1/s which as much as I know is the Hz

There is a lot of (public) confusion here.
The unit, [rad], does not exist as SI-unit. So the unit as for ω is simply [s^-1 ]. But people are just writing [ rad/s ] to clarify the meaning. Also Hz has the unit [ s^-1 ], but here [ rounds/s ] or [periods/s] is meant. So as for myself I prefer [ rad/s ] = [ s^-1 ] and [ Hz ] = [ Hz ]. If all people agreed that, no confusion would exist about this.

So your attached equation is ok: [ rad/s ] = [ 1/s ].

 

[stedwards]

I had a similar issue concerning moles in taking chemistry classes. I found it very useful to assume mole as a unit in order to balance chemical formula. A mole is another example of a "count", as bigyellowhat points out.

It has been assign an System International unit, as has a radian. http://en.wikipedia.org/wiki/Mole_(unit)#The_mole_as_a_unit

 

[hackYou]

Thank you for the answers.
Now I'm even more confused. Every where is stated that the unit for angle is radia. What exactly do you guys mean with it s not a SI unit?

Hesch, unfortunately i can t just set rad = 1/s because i m facing a problem where these two units(?) yield different results where the rad/sec one seems to be closer to the desired output.

 

[Hesch]

Hesch, unfortunately i can t just set rad = 1/s

I've not written that rad = 1/s, but that [rad] is not a SI-unit and thus [rad/s] = [1/s] = [s^-1].

 

[BiGyElLoWhAt]

rad $\neq$ 1/s
rad/s = 1/s
As for the unit of the angle issue, a radian is a ratio of a circle, by a factor of 2 pi, which is unitless, 1 circle is unitless, and 1 radian is the angle encompassed by 1 radius' worth of circumference.

 

[hackYou]

I've not written that rad = 1/s, but that [rad] is not a SI-unit and thus [rad/s] = [1/s] = [s^-1].

I've not written that rad = 1/s, but that [rad] is not a SI-unit and thus [rad/s] = [1/s] = [s^-1].

That's what I meant. I was writing from my phone and made that mistake. Thanks for the input.

 

[hackYou]

Well if you say that rad/s = 1/s which in terms is equal to Hz. How do you explain these formulas taken from another website? Or am I missing the point completely?

1 rad/s = 1/2π Hz = 0.1591549 Hz or 1 Hz = 2π rad/s = 6.2831853 rad/s

 

[BiGyElLoWhAt]

The only difference is a unitless scalar multiple. Hz is frequency and angular velocity equals 2 pi times frequency.

 

[Hesch]

1 rad/s = 1/2π Hz = 0.1591549 Hz or 1 Hz = 2π rad/s = 6.2831853 rad/s

Well, these formulas are correct, but you can do a interesting proof:

1 Hz = 6.28 rad/s , [Hz] = [s^-1] , [rad/s] = [s^-1] →

1 [s^-1] = 6.28 [s^-1] →

6.28 = 1

Confusing ?

 

[stedwards]

Well, these formulas are correct, but you can do a interesting proof:

1 Hz = 6.28 rad/s , [Hz] = [s^-1] , [rad/s] = [s^-1] →

1 [s^-1] = 6.28 [s^-1] →

6.28 = 1

Confusing ?

I think what we are dealing with can be understood in terms of "reduced" vs. "exact" units. My terms. In "reduced units", dimensionless units may be omitted. Note that, units of Hertz replace the older units of cycles/second.

If it confuses problem solving to omit units, include them. There are no hard and fast rules. If the final result must omit radians from the answer, remove them in the last step.

 

[hackYou]

I think what we are dealing with can be understood in terms of "reduced" vs. "exact" units. My terms. In "reduced units", dimensionless units may be omitted. Note that, units of Hertz replace the older units of cycles/second.

If it confuses problem solving to omit units, include them. There are no hard and fast rules. If the final result must omit radians from the answer, remove them in the last step.

Well, my problem(a small but important part of it) is something like this: I have the power output of a shaft and the torque and need to calculate the angular velocity of this shaft. $$ \omega = \frac{P}{T}$$ Like I said, I know the result's units 'are' rad/s. But I never put too much thought into it until now where I'm trying to design a machine with some gears shafts and an electrical motor (stuyding mechanical engineering by the way) and the units don't fit but must be included when I deliver the paper to my mentor.

The thing is that it kinda looks weird to deal with the units like I did on my question (first post) here and at last, when the result comes out as 1/s, just pull a radian out of my ass and make it rad/s!

NOTE. This is not part of any homework. I need this for a university project.

Thank you for your answers.

 

[Hesch]

the units don't fit but must be included

ω = P / T →
s^-1 = ( J/s ) / (N*m )) = ( J/s ) / J = s^-1

The unit [ Nm ] is the unit for torque and for energy.

J = kgm² / s²

N = kgm / s²

 

[hackYou]

ω = P / T →
s^-1 = ( J/s ) / (N*m )) = ( J/s ) / J = s^-1

I need the result to be in radians/s because this is only one part of a more complex calculation that follows and the end result is (if i use 1/s as units) a shaft with a diameter of 40 cm, which is a BS size (huge).

Let's keep it simple (i don't want to post my whole project here) and take it only one step further. Say how would I calculate the velocity of this shaft in rpm if I have the power of the shaft something like 2 or 3 (kW) or whatever and the torque 5 (Nm) for example.

Thank you.

 

[Hesch]

I need the result to be in radians/s

The result is in [rad/s] = [s^-1]

Say how would I calculate the velocity of this shaft in rpm if I have the power of the shaft something like 2 or 3 or whatever and the torque 5 for example.

P = 3W , T = 5 Nm.

ω = P / T = 0.6 [s^-1]

0.6 [s^-1] = 60 [s/min] * 0.6 [s^-1] / 2π = 5.73 rpm

 

[hackYou]

The result is in [rad/s] = [s^-1]

P = 3W , T = 5 Nm.

ω = P / T = 0.6 [s^-1]

0.6 [s^-1] = 60 [s/min] * 0.6 [s^-1] / 2π = 5.73 rpm

Thank you but I'm still not getting the hang of it. It's exactly the same thing happening to my calculations too. This rpm value you calculated seems a little too big. The same goes for my shaft (no pun intended). But when I use the these online calculators for Hz to rad/s the result I get seems more reasonable.

I don't know if I can post links of other sites here. When i use the online calc. from convertunits.com I get 3.769 as a result!
This is driving me nuts!

Again, thnx for the reply.

 

[stedwards]

Yes. Enough philosphy. (lol) You want this.

\omega [rad/s] = \frac{P[J/s]}{T[J/rad]}

Torque is an angular quantity, after all.

 

[hackYou]

Yes. Enough philosphy. (lol) You want this.

\omega [rad/s] = \frac{P[J/s]}{T[J/rad]}

Torque is an angular quantity, after all.

OK. This makes sense. I could(should) have figured out that much myself. The recent days were certainly not my best.

Thank you.

 

[JR Jonsson]

I think you are clever.
Obviously there is an error in the conventions when energy equals torque.
Torque should have the unit Nm/rad.
That could be acceptable if radius defines as m/rad

 

[Chestermiller]

I think you are clever.
Obviously there is an error in the conventions when energy equals torque.
Torque should have the unit Nm/rad.
That could be acceptable if radius defines as m/rad

You are aware that no one has responded to this thread in over a year, right?

 

[JR Jonsson]

Yes