I Why is Stoke's theorem of a closed path equal to zero?

[Phylosopher]

Hello,I had a discussion with my professor. He tried to convince me but I couldn't understand the idea.

The Stokes Theorem (Curl Theorem) is the following:

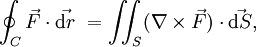
My professor says that the value of the equation should be zero whenever the area of integration is closed! (which will make a volume in that sense!)

He tried to explain that if the area isn't closed then the current on the edge (closed path) of the shape can be represented thoroughly via a closed path integral without going into the whole let's say "infinitesimal currents inside the area"

Moreover, for a closed area there is no edge "closed path" where we can determine the current flow. Here is the problem, logically I find no answer to the problem sense there is no edges that contain the area, meanwhile he says the answer is zero which mean there is no flow.

Also, why can't we just chose a closed path on that closed area and find the answer from it

This might be a really basic "silly" question, I'm sorry but couldn't find any related thoughts in the web about Stokes' and Closed area.

 

[jtbell]

My professor says that the value of the equation should be zero whenever the area of integration is closed!

This is true only if $\vec F$ is a conservative field. In fact, this is how a conservative field is defined.

 

[Phylosopher]

This is true only if $\vec F$ is a conservative field. In fact, this is how a conservative field is defined.

That's true sir, But its not the issue.

My problem is with the thought that the equation (stokes theorem) equal to zero over a closed surface (not path/line).
Am I confused with the definition? -- I'll try to read more on the topic

Thanks for your kind reply

 

[stevendaryl]

I'm not sure I understand what your question is, but maybe I can clarify the situation by taking the example of the surface of a sphere. Say the Earth.

Let \vec{V} be some vector field on the Earth, say the wind velocity. The curl of \vec{V} is nonzero if wind is blowing in a circle (as it does in a hurricane). \nabla \times \vec{V} is directed radially inward (toward the center of the Earth) if the wind is blowing clockwise, and is directed radially outward (away from the center of the Earth) if the wind is blowing counterclockwise. So you can (for whatever reason) compute the average over all the surface of the Earth of the value of the radially outward curl of \vec{V}. Stokes theorem tells you that it has to be zero, since the surface of the Earth is a closed surface.

How can we see that? Well, there are several ways to see it. One way is to break up the surface of the Earth into two hemispheres, the northern hemisphere and the southern hemisphere. The boundary of both of them is the equator. Stokes theorem applied to the northern hemisphere gives us the following equation:

\int_{equator} \vec{V} \cdot \vec{dr} = \int_{north} (\nabla \times \vec{V}) \cdot \vec{dS}

If you integrate \vec{V} along the equator in a counter-clockwise direction (that is, moving east), you'll get the same answer as integrating \nabla \times \vec{V} over the surface of the Earth north of the equator.

Similarly, if you integrate \vec{V} along the equator in a clockwise direction (that is, moving west), you'll get the same answer as integrating \nabla \times \vec{V} over the surface of the Earth south of the equator.

If you add the two integrals together, you'll get the integral of \nabla \times \vec{V} over the entire surface of the Earth--both northern and southern hemispheres. But clearly, adding the two line integrals gives zero, since you're integrating the same function counterclockwise and then clockwise (you just flip the sign of \vec{dr} to go from one integral to the other). This implies that the integral over the entire surface of the Earth of \nabla \times \vec{V} must give zero.

This kind of cancellation of line integrals integrated in opposite directions is the way you can prove Stoke's theorem, in the first place.

 

[lavinia]

If the surface is closed one can use the divergence theorem. The divergence of the curl of a vector field is zero.

Intuitively if the total flux of the curl of a vector field over a surface is the work done against the field along the boundary of the surface then the total flux must be zero if the boundary is empty.

 

[Phylosopher]

I'm not sure I understand what your question is, but maybe I can clarify the situation by taking the example of the surface of a sphere. Say the Earth.

Let \vec{V} be some vector field on the Earth, say the wind velocity. The curl of \vec{V} is nonzero if wind is blowing in a circle (as it does in a hurricane). \nabla \times \vec{V} is directed radially inward (toward the center of the Earth) if the wind is blowing clockwise, and is directed radially outward (away from the center of the Earth) if the wind is blowing counterclockwise. So you can (for whatever reason) compute the average over all the surface of the Earth of the value of the radially outward curl of \vec{V}. Stokes theorem tells you that it has to be zero, since the surface of the Earth is a closed surface.

How can we see that? Well, there are several ways to see it. One way is to break up the surface of the Earth into two hemispheres, the northern hemisphere and the southern hemisphere. The boundary of both of them is the equator. Stokes theorem applied to the northern hemisphere gives us the following equation:

\int_{equator} \vec{V} \cdot \vec{dr} = \int_{north} (\nabla \times \vec{V}) \cdot \vec{dS}

If you integrate \vec{V} along the equator in a counter-clockwise direction (that is, moving east), you'll get the same answer as integrating \nabla \times \vec{V} over the surface of the Earth north of the equator.

Similarly, if you integrate \vec{V} along the equator in a clockwise direction (that is, moving west), you'll get the same answer as integrating \nabla \times \vec{V} over the surface of the Earth south of the equator.

If you add the two integrals together, you'll get the integral of \nabla \times \vec{V} over the entire surface of the Earth--both northern and southern hemispheres. But clearly, adding the two line integrals gives zero, since you're integrating the same function counterclockwise and then clockwise (you just flip the sign of \vec{dr} to go from one integral to the other). This implies that the integral over the entire surface of the Earth of \nabla \times \vec{V} must give zero.

This kind of cancellation of line integrals integrated in opposite directions is the way you can prove Stoke's theorem, in the first place.

Thank you sir, that's exactly the type of explanation I needed to hear.

 

[vanhees71]

Your professor is right, and the reason is trivial. A closed surface has no boundary, and in Stokes's theorem the curve $C$ on the left-hand side is the boundary of the surface $S$ on the right-hand side, $C=\partial S$. For a closed surface $\partial S=\{ \}$.

Another thing is the question whether you have a conserved vector field or not. This is more subtle, but then $S$ is necessarily not closed and has a boundary curve $\partial S$. In a simply connected space the vector field is conserved if $\vec{\nabla} \times \vec{F}=0$ since then you can choose some arbitrary fixed point $\vec{x}_0$ and an arbitrary path $C(\vec{x},\vec{x}_0)$ connecting the points $\vec{x}$ and $\vec{x}_0$. Then according to Stokes's theorem the potential
$$V(\vec{x})=-\int_{C(\vec{x},\vec{x}_0)} \mathrm{d} \vec{r} \cdot \vec{F}$$
is independent of the choice of the path and fulfills
$$\vec{F}=-\vec{\nabla} V.$$
It is important to keep in mind that this is valid only in simply connected domains. A counterexample is the potential vertex
$$\vec{F}=\frac{1}{\sqrt{x^2+y^2}} \begin{pmatrix} y \\ -x \\0 \end{pmatrix}.$$
This vector field is defined everywhere except along the $z$ axis, i.e., in a multiply connected region, and the integral along any closed curved around the $z$ axis is non-zero. Nevertheless, there's a potential locally around any point not on the $z$ axis since $\vec{\nabla} \times \vec{F} \neq 0$ everywhere except along the $z$ axis.

 

[lavinia]

Your professor is right, and the reason is trivial. A closed surface has no boundary, and in Stokes's theorem the curve $C$ on the left-hand side is the boundary of the surface $S$ on the right-hand side, $C=\partial S$. For a closed surface $\partial S=\{ \}$.

Can you explain why it is trivial?

I think Stevendaryl's explanation in post #4 is not trivial and it gives deep insight into why the theorem is true.

Also in Post #5 where one uses the Divergence Theorem seems to be non-trivial.

I don't see why the proof of Stokes Theorem accounts for the case of empty boundary. Every proof that I have seen assumes that the boundary is non-empty.

 

[vanhees71]

Well, isn't the statement that the boundary of a closed surface is just empty? Stevendaryl answered a different question since he understood your question in a different way than I did. Of course Stokes's and Gauss's theorems themselves are not trivial.

 

[lavinia]

Well, isn't the statement that the boundary of a closed surface is just empty? Stevendaryl answered a different question since he understood your question in a different way than I did. Of course Stokes's and Gauss's theorems themselves are not trivial.

There were two proofs. Stevendaryl's proof divides the closed surface into two regions, He then uses Stokes Theorem to reduce the integral of the curl of the vector field over each of the regions to the integral of the vector field over their common boundary. These integrals occur with opposite orientations so the two boundary integrals cancel. This proof requires knowing Stokes Theorem for the case of a non-trivial boundary.

The other proof uses the Divergence Theorem. This again is a case of Stokes theorem for a region with a non-empty boundary. This proof seems less general than Setvendaryl's since on a general manifold the closed surface may not be the boundary of a solid region. In Euclidean space a hypersurface does bound but this is not easy to prove and on a general manifold it is not always true.