Dr. Who
- 9
- 0
Question:-
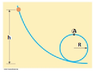
A bead slides without friction around a loop-the-loop (Please click on the below link for diagram). The bead is released from a height h = 3.50R. (a) What is its speed at point A? (b) How large is the normal force on it if its mass is 5.00 g?
https://www.dropbox.com/s/wsd8g5q9d87undj/Loop Quest.png?dl=0
v = √29.4R
(b)
Similarly, I don't at all understand the equation for part(b) of the problem. Please explain your solutions with inline comments.
Thanks in advance! :)https://www.dropbox.com/s/wsd8g5q9d87undj/Loop%20Quest.png?dl=0
A bead slides without friction around a loop-the-loop (Please click on the below link for diagram). The bead is released from a height h = 3.50R. (a) What is its speed at point A? (b) How large is the normal force on it if its mass is 5.00 g?
https://www.dropbox.com/s/wsd8g5q9d87undj/Loop Quest.png?dl=0
Homework Equations
(a) Potential Energy( at height 'h')=Kinetic Energy( at A)+Potential Energy( at A)
(b) Normal force + Weight of the bead = Centripetal force
(b) Normal force + Weight of the bead = Centripetal force
The Attempt at a Solution
(a)
mgh=(½ mv2) + mghA
gh= (½ v2) + ghA
v2=2g( h- hA )=2(9.8)(3.5R-2R)=29.4Rgh= (½ v2) + ghA
v = √29.4R
N + mg = (mv2)/R
N = m {(v2/R)-(g)}
N = 0.005 {(29.4R/R)-(9.8)}
N = 0.098
My Professor has suggested the above solution but I want to know how can you take the height at point A to be 2R?N = m {(v2/R)-(g)}
N = 0.005 {(29.4R/R)-(9.8)}
N = 0.098
Similarly, I don't at all understand the equation for part(b) of the problem. Please explain your solutions with inline comments.
Thanks in advance! :)https://www.dropbox.com/s/wsd8g5q9d87undj/Loop%20Quest.png?dl=0
Last edited by a moderator: