Very strange! (Sorry about that.)
I'll try to cut and paste the section, see if it works:
Flux
The electric field is a vector field. It is a quantity with magnitude and direction defined at every point in space. Another example of a vector field that is easier to visualize is the velocity of water in a stream. The flux of a vector field through a surface area is the amount of whatever the field represents passing through the area. The total flux depends on strength of the field, the size of the surface area it passes through, and on how the area is oriented with respect to the field. You can think of flux as the amount of something crossing a surface. The surface is a two dimensional (real or imagined) boundary. It can be open or closed. An open surface could be a the area of a door, the area of a sheet of paper, the area of a bowl, etc. A closed surface could be the surface are of a sphere or a cube, etc. Flux is measure at a single point in time. Flux is the total amount of something crossing the surface, it is not something per unit area, etc.
Field lines help us to visualize the electric field. The density of the field lines is proportional to the strength of the field.
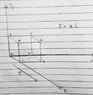
View attachment 264633The number of field lines passing through a geometrical surface of given area A depends on three factors.
- the strength of the field
- the surface area
- the orientation of the surface
The number of field lines passing through an area A is proportional to the flux through that area.
The diagram on the right shows a locally uniform electric field
E. The lines are parallel and have constant density. The same surface is inserted in three different orientations. The maximum number of field lines is intercepted when unit vector normal to the surface,
n, is parallel to the field
E, while no field lines pass through the surface when
n is perpendicular to the field. In general, the number of field lines passing through an area A is directly proportional to A*cosθ, where θ is the angle between the field direction and the unit vector
n normal to the surface. This leads to the definition of the
electric flux.
ΔΦE = E ΔA cosθ.
ΔΦE is the electric flux through some small area ΔA, whose normal make an angle θ with the direction of the electric field. E is the magnitude of the field. The SI unit of flux is Nm2/C.
E is a vector quantity. It is useful also to represent the area A by a vector
A. The length of this vector is the size of the area, while its orientation is perpendicular to the area. It is in the direction of the normal
n. We have
A = A
n. The normal to the surface can point into two different directions.
For a closed surface, by convention, the normal points outward. With our definition of
A we can write the flux as the dot product of
E and Δ
A.
ΔΦE =
E∙Δ
A = Eperpendicular*ΔA = E ΔA cosθ.
ΔΦE is the flux through a small are ΔA, which may be part of a larger area A. The total electric flux ΦE through A can be evaluated by summing the differential flux over the all elements of surface A,
ΦE= ∑ΔA -> 0 Eperpendicular ΔA = ∑ΔA -> 0
E∙Δ
A.
View attachment 264634The flux through a given surface can be positive or negative, since the cosine can be positive or negative. The flux through a closed surface is positive if there is a net outward flow, and negative if there is a net inward flow. We have a net outward flux if there is a source inside the closed surface and a net inward flux if there is a sink inside the closed surface.
Consider the electrical flux passing through a cubical surface with two of its faces perpendicular to a uniform electrical field. The flux passing through the top, bottom, front, and back sides of the cube is zero since these sides are parallel to the field lines and thus do not intercept any of them. The normal vector
n is perpendicular to the field for these sides and cosθ is zero. As drawn, the field lines are parallel to the normal vector
n for the right side, so the flux through this side is ΦE = EA. The field lines are anti-parallel to the normal vector
n for the left side, so the flux through this side is ΦE = -EA. The total flux through the surface of the cube is the sum of the fluxes through all sides, and it is zero.
The flux of a vector field through a closed surface is always zero if there is no source or sink of the vector field in the volume enclosed by the surface. The sources and sinks for the electric field are charges.
The flux of a electric field through a closed surface is always zero if there is no net charge in the volume enclosed by the surface.