eognvoi
- 1
- 0
Summary:: Figure b also shows that there is no negative sign in Faraday's Law. How do I know when to include the negative sign?
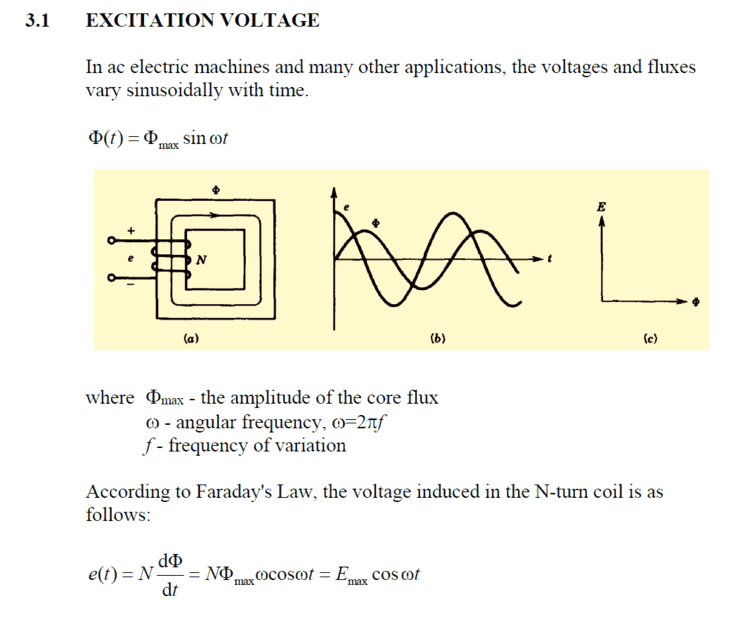
The discussion centers on the absence of a negative sign in Faraday's Law as presented in certain contexts. Participants agree that the negative sign is essential due to Lenz's Law, which states that the induced electromotive force (emf) generates a current opposing the change in magnetic flux. References to Wikipedia and Hyperphysics confirm the necessity of the negative sign for consistency in electromagnetic theory. The conversation emphasizes that using the term "voltage" in relation to Faraday's Law can lead to misunderstandings, as it implies a potential difference that does not exist in time-varying magnetic fields.
PREREQUISITESPhysics students, electrical engineers, educators, and anyone interested in the principles of electromagnetism and their applications in technology.
Is this the "conversation" you were thinking of?kuruman said:I remember having this conversation about voltage here at PF a number of years ago, but I could not find the link.
Just don't use the word "voltage" in connection with Faraday's law, because it's a contradiction in itself. There is no potential when time-varying magnetic fields are present due to Faraday's law:kuruman said:I was under the impression that the term "voltage" is used exclusively to denote the absolute value of the electric potential difference which can be positive of negative. For example, when we say that "the voltage across a capacitor is charge divided by capacitance", all three quantities are positive. In my mind, voltage is to potential difference as distance is to displacement.
I agree that the negative sign in Faraday's law is put there for Lenz's law. It indicates that the induced potential difference is such that it gives rise to an induced current that opposes the proposed change in magnetic flux. I view it as analogous to the negative sign in Hooke's law that indicates that the direction of the force exerted by the spring opposes the proposed deformation of the spring. The direction of an arrow in a free body diagram says it all and a minus sign is not needed. In fact, it would be wrong to label an arrow representing the force due to a spring by "-kx". Similarly, the direction of the induced current in a circuit says it all and a minus sign is not needed.
I remember having this conversation about voltage here at PF a number of years ago, but I could not find the link.