wahaj
- 154
- 2
Homework Statement
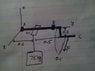
I have to find reaction at the joints but that's not important. I'm having trouble understanding what the book is doing but first allow me to explain the diagram so there is no confusion because 3D pictures are kinda hard to draw. In the first diagram there is a crank shaft running along the y axis. 0.1 m after point B it goes down 0.2 m along the z axis and then 0.1 m along the y axis.A is a thrust bearing and B is a smooth journal bearing
Homework Equations
Statical equilibrium equations apply here
The Attempt at a Solution
When finding the moment about the z axis the equation should look something like this according to me.
Bx(0.5+0.6)- ux x rCA x F = 0
rCA=-0.1i - 1.3j + 0.2k
and ux = i
but here is how the book does it.
Bx(0.5+0.6) - F(0.2+0.1+0.6+0.5) = 0
Now I understand to find the moment about an axis I have to take the force and multiply it by the perpendicular distance between the force and a point on the axis. This works if both the axis and the force lie on one plane. When dealing with multiple planes I have to take the cross product. But I really have no idea why the book is doing what its doing. Can someone tell me if my equation is right or not and also explain why the book simply takes all the distances involved in getting from C to A and adds them without any regard of which axis they follow. Ask for clarification if I did a bad job of explaining.