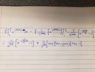You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Engineering Why Multiply by Exponential Terms in Fourier Series Calculations?
- Thread starter lottotlyl
- Start date
AI Thread Summary
Using complex identities for sin(pi*k/3) in Fourier series calculations can be challenging, as demonstrated by the difficulty in applying the fundamental theorem of calculus. The theorem states that the integral of a function can be evaluated using its antiderivative. To simplify the calculations, it's suggested to multiply by the term e^(-j*pi*k/3), which can help in managing the exponential terms in the final answer. This approach integrates elemental algebra and complex analysis to facilitate the process. Understanding these steps is crucial for effective Fourier series computations.
Physics news on Phys.org
Gaussian97
Homework Helper
- 683
- 412
Applying the fundamental theorem of calculus which says that
$$\int_a^b f(t)dt=F(t)\Big|_a^b=F(b)-F(a)$$ where ##F(t)## is a function satisfying $$\frac{dF(t)}{dt}=f(t).$$
Then you also need to use elemental algebra and complex analysis.
$$\int_a^b f(t)dt=F(t)\Big|_a^b=F(b)-F(a)$$ where ##F(t)## is a function satisfying $$\frac{dF(t)}{dt}=f(t).$$
Then you also need to use elemental algebra and complex analysis.
Gaussian97
Homework Helper
- 683
- 412
Well, notice that in the final answer you have the term $$e^{\frac{-j\pi k}{3}}$$ so it would be a good idea to multiply by $$1=e^{\frac{-j\pi k}{3}}e^{\frac{j\pi k}{3}}.$$
Similar threads
- Replies
- 4
- Views
- 6K
Engineering
Fourier transform of a shifted sine wave
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 26
- Views
- 3K
- Replies
- 4
- Views
- 2K
- Replies
- 3
- Views
- 6K
- Replies
- 1
- Views
- 2K
- Replies
- 6
- Views
- 1K
- Replies
- 3
- Views
- 1K
Hot Threads
-
MCNP6 simulation about shielding and mobile xray
- Started by gitagituy
- Replies: 22
- Engineering and Comp Sci Homework Help
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Max water pressure allowable on solar panels
- Started by ethanesh
- Replies: 16
- Engineering and Comp Sci Homework Help
-
Spiral scissor lift statics
- Started by carlcla
- Replies: 4
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 3
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math