Will current take the path of least impedance in this circuit?

Click For Summary
SUMMARY

The discussion focuses on a circuit analysis involving a current source connected to a parallel RL (Resistor-Inductor) circuit and an RC (Resistor-Capacitor) circuit. It concludes that when the current source activates, the current will predominantly flow through the path with no impedance, bypassing the capacitor entirely. Consequently, the current flowing through the inductor will match both the magnitude and phase angle of the current supplied by the current source, confirming the behavior of parallel circuits in terms of impedance.

PREREQUISITES
  • Understanding of RL and RC circuit configurations
  • Knowledge of current sources and their behavior in circuits
  • Familiarity with impedance concepts in electrical engineering
  • Basic principles of circuit analysis, including Kirchhoff's laws
NEXT STEPS
  • Study the characteristics of RL and RC circuits in parallel configurations
  • Learn about impedance calculations in AC circuits
  • Explore the effects of capacitors and inductors on current flow
  • Investigate Kirchhoff's laws for complex circuit analysis
USEFUL FOR

Electrical engineering students, circuit designers, and anyone interested in understanding the behavior of parallel RL and RC circuits in response to current sources.

Juwane
Messages
86
Reaction score
0

Homework Statement



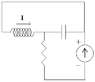
See the circuit in the attached image.

Homework Equations



N/A


Consider the circuit given in the attached image, then please answer the following questions:

1. When the current will come out of the current source, will all that current will go through the path with no impedance above, and none of it will go through the capacitor?

2. If the answer to the above question is yes, then will the current flowing through the inductor be exactly the same current (both magnitude and angle) as the current given by the current source?
 

Attachments

  • least resistance.gif
    least resistance.gif
    1.7 KB · Views: 578
Physics news on Phys.org
This circuit is basically a RL circuit and a RC circuit connected in parallel. I am not 100% sure, but i think the best direction to go with this is to look back at the properties of both of those kinds of circuits.
 

Similar threads

Current through an inductor as a function of time
  • · Replies 10 ·
Replies
10
Views
1K
Resonant frequency of L - R||C circuit
  • · Replies 21 ·
Replies
21
Views
2K
How to Calculate Energy Stored in an Inductor?
  • · Replies 16 ·
Replies
16
Views
4K
Understanding Short Circuit Current Paths in Electrical Circuits
  • · Replies 4 ·
Replies
4
Views
2K
LC oscillations - two capacitors and an inductor
  • · Replies 15 ·
Replies
15
Views
1K
Determining Inductance L in an LC Circuit
  • · Replies 5 ·
Replies
5
Views
2K
Calculation of current in driven series RLC circuit
  • · Replies 8 ·
Replies
8
Views
3K
Why Do Capacitors Behave Differently in Series and Parallel Configurations?
  • · Replies 20 ·
Replies
20
Views
2K
Current flowing through a resistor in an RRL DC circuit
  • · Replies 5 ·
Replies
5
Views
2K
Combined tensions of an RLC series circuit with AC current
  • · Replies 3 ·
Replies
3
Views
1K